题目内容
求下列函数图象的对称轴、顶点坐标及与x轴的交点坐标．
（1）y=x2-2x+3； （2）y=-3x2+6x+2．
解：对于y=ax2+bx+c，其顶点坐标为（-
，
），于是：
（1）y=x2-2x+3的对称轴为x=-
=1；顶点纵坐标为
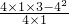=-1
则其顶点坐标为（1，-1）；
当y=0时，x2-2x+3=0，△=4-4×1×3=-8＜0，函数图象与x轴无交点．
（2）y=-3x2+6x+2的对称轴为x=-
=1；顶点纵坐标为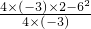
=5，
则其顶点坐标为（1，5）；
当y=0时，-3x2+6x+2=0，△=36-4×（-3）×2=60，
x1=1+
；x1=1-．
故函数图象与x轴的交点坐标为（1+，0）（1-，0）．
分析：由于（1）、（2）均为二次函数一般式，利用二次函数顶点坐标公式可直接求出对称轴及顶点坐标；令y=0，将函数转化为关于x的一元二次方程，方程的解即为抛物线与x轴的交点坐标．
点评：本题考查了抛物线与x轴的交点及二次函数的性质，知道函数与x轴的交点横坐标是相应方程的解是解题的关键．
，），于是：（1）y=x2-2x+3的对称轴为x=-
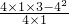=1；顶点纵坐标为=-1则其顶点坐标为（1，-1）；
当y=0时，x2-2x+3=0，△=4-4×1×3=-8＜0，函数图象与x轴无交点．
（2）y=-3x2+6x+2的对称轴为x=-
=1；顶点纵坐标为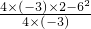=5，则其顶点坐标为（1，5）；
当y=0时，-3x2+6x+2=0，△=36-4×（-3）×2=60，
x1=1+
；x1=1-．故函数图象与x轴的交点坐标为（1+
，0）（1-，0）．分析：由于（1）、（2）均为二次函数一般式，利用二次函数顶点坐标公式可直接求出对称轴及顶点坐标；令y=0，将函数转化为关于x的一元二次方程，方程的解即为抛物线与x轴的交点坐标．
点评：本题考查了抛物线与x轴的交点及二次函数的性质，知道函数与x轴的交点横坐标是相应方程的解是解题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
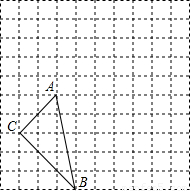
（2011•安宁市一模）在如图所示的方格纸中，每个小正方形的边长都为1．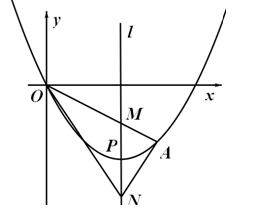
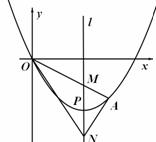OA交其对称轴
于点M，点M、N关于点P对称，连接AN、ON
于点M，点M、N关于点P对称，连接AN、ON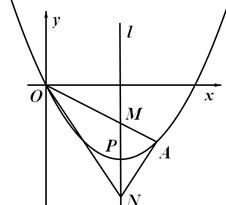
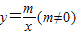的图象的一支恰好经过点C2，求此反比例函数解析式．