题目内容
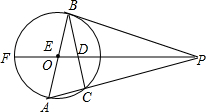 (1997•湖南)已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠APB是平分线分别交BC,AB于点D、E,交⊙O于点F,∠A=60°,并且线段AE、BD的长是一元二次方程 x2-kx+2
(1997•湖南)已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠APB是平分线分别交BC,AB于点D、E,交⊙O于点F,∠A=60°,并且线段AE、BD的长是一元二次方程 x2-kx+2| 3 |
(1)求证:PA•BD=PB•AE;
(2)求证:⊙O的直径长为常数k;
(3)求tan∠FPA的值.
分析:(1)由PB切⊙O于点B,根据弦切角定理,可得∠PBD=∠A,又由PF平分∠APB,可证得△PBD∽△PAE,然后由相似三角形的对应边成比例,证得PA•BD=PB•AE;
(2)易证得BE=BD,又由线段AE、BD的长是一元二次方程 x2-kx+2
=0的两根(k为常数),即可得AE+BD=k,继而求得AB=k,即:⊙O的直径长为常数k;
(3)由∠A=60°,并且线段AE、BC的长是一元二次方程 x2-kx+2
=0的两根(k为常数),可求得AE与BD的长,继而求得tan∠FPB的值,则可得tan∠FPA的值.
(2)易证得BE=BD,又由线段AE、BD的长是一元二次方程 x2-kx+2
| 3 |
(3)由∠A=60°,并且线段AE、BC的长是一元二次方程 x2-kx+2
| 3 |
解答:(1)证明:如图,
∵PB切⊙O于点B,
∴∠PBD=∠A,
∵PF平分∠APB,
∴∠APE=∠BPD,
∴△PBD∽△PAE,
∴PB:PA=BD:AE,
∴PA•BD=PB•AE;(2分)
(2)证明:如图,
∵∠BED=∠A+∠EPA,∠BDE=∠PBD+∠BPD.
又∵∠PBD=∠A,∠EPA=∠BPD,
∴∠BED=∠BDE.
∴BE=BD.
∵线段AE、BD的长是一元二次方程 x2-kx+2
=0的两根(k为常数),
∴AE+BD=k,
∴AE+BD=AE+BE=AB=k,
即⊙O直径为常数k.(5分)
(3)∵PB切⊙O于B点,AB为直径.
∴∠PBA=90°.
∵∠A=60°.
∴PB=PA•sin60°=
PA,
又∵PA•BD=PB•AE,
∴BD=
AE,
∵线段AE、BD的长是一元二次方程 x2-kx+2
=0的两根(k为常数).
∴AE•BD=2
,
即
AE2=2
,
解得:AE=2,BD=
,
∴AB=k=AE+BD=2+
,BE=BD=
,
在Rt△PBA中,PB=AB•tan60°=(2+
)×
=3+2
.
在Rt△PBE中,tan∠BPF=
=
=2-
,
∵∠FPA=∠BPF,
∴tan∠FPA=2-
.
∵PB切⊙O于点B,
∴∠PBD=∠A,
∵PF平分∠APB,
∴∠APE=∠BPD,
∴△PBD∽△PAE,
∴PB:PA=BD:AE,
∴PA•BD=PB•AE;(2分)
(2)证明:如图,
∵∠BED=∠A+∠EPA,∠BDE=∠PBD+∠BPD.
又∵∠PBD=∠A,∠EPA=∠BPD,
∴∠BED=∠BDE.
∴BE=BD.
∵线段AE、BD的长是一元二次方程 x2-kx+2
| 3 |
∴AE+BD=k,
∴AE+BD=AE+BE=AB=k,
即⊙O直径为常数k.(5分)
(3)∵PB切⊙O于B点,AB为直径.
∴∠PBA=90°.
∵∠A=60°.
∴PB=PA•sin60°=
| ||
| 2 |
又∵PA•BD=PB•AE,
∴BD=
| ||
| 2 |
∵线段AE、BD的长是一元二次方程 x2-kx+2
| 3 |
∴AE•BD=2
| 3 |
即
| ||
| 2 |
| 3 |
解得:AE=2,BD=
| 3 |
∴AB=k=AE+BD=2+
| 3 |
| 3 |
在Rt△PBA中,PB=AB•tan60°=(2+
| 3 |
| 3 |
| 3 |
在Rt△PBE中,tan∠BPF=
| BE |
| PB |
| ||
3+2
|
| 3 |
∵∠FPA=∠BPF,
∴tan∠FPA=2-
| 3 |
点评:此题考查了切线的性质、等腰三角形的判定与性质、相似三角形的判定与性质以及根与系数的关系等知识.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (1997•湖南)已知:线段m,n(如图).求作:△ABC,使AB=AC,且BC=m,高AD=n.(要求写出作法,不写证明)
(1997•湖南)已知:线段m,n(如图).求作:△ABC,使AB=AC,且BC=m,高AD=n.(要求写出作法,不写证明) (1997•湖南)已知:如图,在矩形ABCD中,BE=DF.求证:AF=CE.
(1997•湖南)已知:如图,在矩形ABCD中,BE=DF.求证:AF=CE.