Question

【题目】如图，在平面直角坐标系中，矩形的顶点在轴正半轴上，边，（）的长分别是方程的两个根，是边上的一动点（不与A、B重合）.

（1）填空：AB=　 　，OA=　 　．

（2）若动点D满足△BOC与△AOD相似，求直线的解析式.

（3）若动点D满足，且点为射线上的一个动点，当△PAD是等腰三角形时，直接写出点的坐标．

Answer 1

【答案】（1）8,3;(2) ; (3) 点的坐标为(0,0)，，，．

【解析】

（1）解方程求得方程的两根即可由题意求得AB、OA的长度；

（2）由题意可知∠OCB=∠OAD=90°，由此可知若△BOC与△AOD相似，则存在若①△BOC∽△DOA；②△BOC∽△ODA两种情况，根据这两种情况结合已知条件分析解答即可；

（3）由已知易得AD=AO=3，然后根据题意分①AD=AP1；②AD=P2D；③AP3=DP3；④AD=P4D，共4种情况结合已知条件分析解答即可.

（1）解方程得：，

∵AB>AO，

∴AB=8，AO=3；

（2）∵四边形OABC是矩形，

∴∠OCB=∠OAD=90°，

∴若△BOC与△AOD相似，则存在若①△BOC∽△DOA；②△BOC∽△ODA两种情况，

①若△BOC∽△DOA.

则 ，即，

解得： ；

②若△BOC∽△ODA，可得AD=8（与题意不符，舍去），

设直线解析式为，则，

解得：，

∴直线的解析式为．

（3）∵AD+DB=AB=8， ，

∴，

∵，

∴是等腰直角三角形，

∴，，

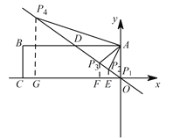
根据△PAD是等腰三角形，分以下4种情况讨论：

①如下图所示，

当时，点的坐标为；

②如下图所示，当DA=DP2=3时，过P2E作x轴的垂线，垂足为E，

则，△OEP2是等腰直角三角形，

∴，

∴点的坐标为　；

③如下图所示，当时，，

∴△ADP3是等腰直角三角形，

∴，

∴，

过作轴的垂线，垂足为，则△OP3F是等腰直角三角形，

∴，

∴点的坐标为；

④如下图所示，当时，，

过作轴的垂线，垂足为，则是等腰直角三角形，

∴，

∴点的坐标为；

综上所述，当△PAD是等腰三角形时，点的坐标为，，，．