题目内容
从2开始,连续的正偶数相加,它们的和的情况如下表,当n个最小的连续正偶数相加时,它们的和记为s
(1)根据表中规律,用n表示s的代数式;
(2)利用(1)的结论,求2+4+6+…+202的值;
(3)利用(1)的结论,求126+128+130+…+300的值.
(1)根据表中规律,用n表示s的代数式;
(2)利用(1)的结论,求2+4+6+…+202的值;
(3)利用(1)的结论,求126+128+130+…+300的值.
| 加数的个数(n) | 和(S) |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
| … | … |
(1)s=n(n+1);
(2)s=101×(101+1)=10302;
(3)126+128+130+…+300,
=(2+4+6+…+300)-(2+4+6+…+124)
=150×(150+1)-62×(62+1)=18744.
(2)s=101×(101+1)=10302;
(3)126+128+130+…+300,
=(2+4+6+…+300)-(2+4+6+…+124)
=150×(150+1)-62×(62+1)=18744.

练习册系列答案
相关题目
从2开始,连续的正偶数相加,它们的和的情况如下表,当n个最小的连续正偶数相加时,它们的和记为s
(1)根据表中规律,用n表示s的代数式;
(2)利用(1)的结论,求2+4+6+…+202的值;
(3)利用(1)的结论,求126+128+130+…+300的值.
| 加数的个数(n) | 和(S) |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
| … | … |
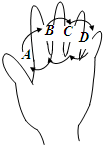 如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从开始数连续的正整数1、2、3、4…,当字母C第2011次出现时,恰好数到的数是
如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从开始数连续的正整数1、2、3、4…,当字母C第2011次出现时,恰好数到的数是 到的数(提示:2n+1=101).
到的数(提示:2n+1=101).