题目内容
 (2013•昌平区二模)如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为1,则?ABCD的面积为
(2013•昌平区二模)如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为1,则?ABCD的面积为12
12
.分析:求出CE=3DE,AB=2DE,求出
=
,
=
,根据平行四边形的性质得出AB∥CD,AD∥BC,推出△DEF∽△CEB,△DEF∽△ABF,求出
=(
)2=
,
=(
)2=
,求出△CEB的面积是9,△ABF的面积是4,得出四边形BCDF的面积是8,即可得出平行四边形ABCD的面积.
| DE |
| CE |
| 1 |
| 3 |
| DE |
| AB |
| 1 |
| 2 |
| S△DEF |
| S△CEB |
| DE |
| EC |
| 1 |
| 9 |
| S△DEF |
| S△ABF |
| DE |
| AB |
| 1 |
| 4 |
解答:解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵CD=2DE,
∴CE=3DE,AB=2DE,
∴
=
,
=
,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△DEF∽△CEB,△DEF∽△ABF,
∴
=(
)2=
,
=(
)2=
,
∵△DEF的面积为1,
∴△CEB的面积是9,△ABF的面积是4,
∴四边形BCDF的面积是9-1=8,
∴平行四边形ABCD的面积是8+4=12,
故答案为:12.
∴AD=BC,AB=CD,
∵CD=2DE,
∴CE=3DE,AB=2DE,
∴
| DE |
| CE |
| 1 |
| 3 |
| DE |
| AB |
| 1 |
| 2 |
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△DEF∽△CEB,△DEF∽△ABF,
∴
| S△DEF |
| S△CEB |
| DE |
| EC |
| 1 |
| 9 |
| S△DEF |
| S△ABF |
| DE |
| AB |
| 1 |
| 4 |
∵△DEF的面积为1,
∴△CEB的面积是9,△ABF的面积是4,
∴四边形BCDF的面积是9-1=8,
∴平行四边形ABCD的面积是8+4=12,
故答案为:12.
点评:本题考查了平行四边形性质,相似三角形的性质和判定的应用,注意:相似三角形的面积比等于相似比的平方.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 (2013•昌平区二模)如图,AC∥FE,点F、C在BD上,AC=DF,BC=EF.
(2013•昌平区二模)如图,AC∥FE,点F、C在BD上,AC=DF,BC=EF. (2013•昌平区二模)在水平的讲台桌上放置圆柱形笔筒和长方体形粉笔盒(如图),则它的主视图是( )
(2013•昌平区二模)在水平的讲台桌上放置圆柱形笔筒和长方体形粉笔盒(如图),则它的主视图是( )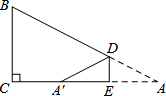 (2013•昌平区二模)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
(2013•昌平区二模)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( ) (2013•昌平区二模)正三角形ABC的边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC2,则y关于x的函数的图象大致为( )
(2013•昌平区二模)正三角形ABC的边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC2,则y关于x的函数的图象大致为( )