Question

【题目】如图，将菱形ABCD放置在平面直角坐标系中，已知A（0，3）．B（﹣4，0）
（1）求经过点C的反比例函数解析式；
（2）设P是（1）中所求函数图象上的一点，以P、O、A为顶点的三角形的面积与△COD的面积相等，求点P的坐标．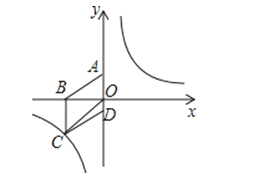

Answer 1

【答案】解：（1）由题意知，OA=3，OB=4
在Rt△AOB中，AB==5
∵四边形ABCD为菱形
∴AD=BC=AB=5，
∴C（﹣4，﹣5）．
设经过点C的反比例函数的解析式为y=（k≠0），
则k=﹣4×﹣5=20．
故所求的反比例函数的解析式为y=．
（2）设P（x，y）
∵AD=AB=5，OA=3，
∴OD=2，S△COD=×4×2=4，
即AO×|x|=4，
∴|x|=，
∴x=±，
当x=时，y=，当x=﹣时，y=﹣，
点P的坐标为（，）或（﹣，﹣）．
【解析】（1）根据菱形的性质可得菱形的边长，进而可得点C的坐标，代入反比例函数解析式可得所求的解析式；
（2）设出点P的坐标，易得△COD的面积，利用点P的横坐标表示出△PAO的面积，那么可得点P的横坐标，就求得了点P的坐标．
【考点精析】本题主要考查了反比例函数的性质的相关知识点，需要掌握性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大才能正确解答此题．