题目内容
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )
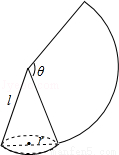
A. 6cm B. 7cm C. 8cm D. 9cm
练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
题目内容
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )

A. 6cm B. 7cm C. 8cm D. 9cm
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案