题目内容
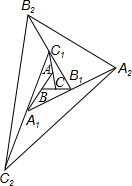 (2012•张家口一模)如图,△ABC的面积为1.分别倍长AB,BC,CA得到△A1B1C1.再分别倍长A1B1,B1C1,C1A1得到△A2B2C2.…按此规律,倍长n次后得到的△AnBnCn的面积为
(2012•张家口一模)如图,△ABC的面积为1.分别倍长AB,BC,CA得到△A1B1C1.再分别倍长A1B1,B1C1,C1A1得到△A2B2C2.…按此规律,倍长n次后得到的△AnBnCn的面积为7n
7n
.分析:根据等底等高的三角形的面积相等可得三角形的中线把三角形分成两个面积相等的三角形,然后求出第一次倍长后△A1B1C1的面积是△ABC的面积的7倍,依此类推写出即可.
解答: 解:连接AB1、BC1、CA1,根据等底等高的三角形面积相等,
解:连接AB1、BC1、CA1,根据等底等高的三角形面积相等,
△A1BC、△A1B1C、△AB1C、△AB1C1、△ABC1、△A1BC1、△ABC的面积都相等,
所以,S△A1B1C1=7S△ABC,
同理S△A2B2C2=7S△A1B1C1,=72S△ABC,
依此类推,S△AnBnCn=7nS△ABC,
∵△ABC的面积为1,
∴S△AnBnCn=7n.
故答案为:7n.
 解:连接AB1、BC1、CA1,根据等底等高的三角形面积相等,
解:连接AB1、BC1、CA1,根据等底等高的三角形面积相等,△A1BC、△A1B1C、△AB1C、△AB1C1、△ABC1、△A1BC1、△ABC的面积都相等,
所以,S△A1B1C1=7S△ABC,
同理S△A2B2C2=7S△A1B1C1,=72S△ABC,
依此类推,S△AnBnCn=7nS△ABC,
∵△ABC的面积为1,
∴S△AnBnCn=7n.
故答案为:7n.
点评:本题考查了三角形的面积,根据等底等高的三角形的面积相等求出一次倍长后所得的三角形的面积等于原三角形的面积的7倍是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
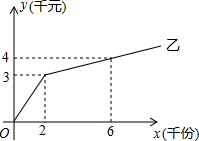 (2012•张家口一模)某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表:
(2012•张家口一模)某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表: (1)求抽取的学生人数,并根据抽查到的学生五个等级人数的分布情况,补全扇形统计图和频数分布直方图;
(1)求抽取的学生人数,并根据抽查到的学生五个等级人数的分布情况,补全扇形统计图和频数分布直方图;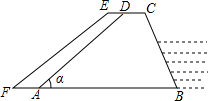 (2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.
(2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.