Question

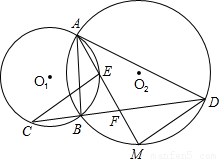
已知：如图，AB是⊙O₁与⊙O₂的公共弦，过B点的直线CD分别交⊙O₁于C点，交⊙O₂于D点，∠BAD的平分线AM交⊙O₁于E点，交直线CD于F点，交⊙O₂于M点．
（1）连接DM、CE，请在图中（不添加别的“点”和“线”）找出与△DFM相似的所有三角形，并选择其中一个三角形，证明它与△DFM相似；
（2）设CD=12，CB=5，DF=4，AF=3FM，求EF的长．

Answer 1

【答案】分析：（1）由已知，∠FDM=∠FAB=∠C，∠DFM=∠CFE，可证△DFM∽△CEF，△DFM∽△AFB，又AM平分∠BAD，即得MDF=∠DAM，又∠M=∠M，易证△DFM∽△ADM，与△DFM相似的三角形有：△CEF、△AFB、△ADM；
（2）根据圆的相交弦定理和圆的切割线定理求解．
解答：解：（1）与△DFM相似的三角形有：△CEF、△AFB、△ADM，（3分）
（少写一个相似三角形扣（1分），扣完为止）
证明：∵∠FDM=∠FAB=∠C，∠DFM=∠CFE，
∴△DFM∽△CEF，△DFM∽△AFB
∵AM平分∠BAD
∴∠DAF=∠FAB
∵∠MDF=∠FAB
∴∠MDF=∠DAM
又∠M=∠M
∴△DFM∽△ADM；（5分）
（只要证明其中一个三角形与△DFM相似即可）

（2）BF=CD-CB-DF=3，
由圆的相交弦定理，得DF•BF=AF•MF，即4×3=3MF²，
解得MF=2，故AF=6，（7分）
由圆的切割线定理，得FE•FA=FB•FC，即6FE=3×8，
解得EF=4．（8分）
点评：此题综合考查了相似三角形的判定、相交弦定理、切割线定理和圆周角定理．