Question

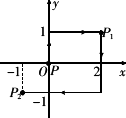
如图，已知O是平面直角坐标系的原点，半径为1的⊙B经过点O，且与x、y

轴分别交于点A、C，点A的坐标为（-，0），AC的延长线与⊙B的切线OD

交于点D.

（1）求OC的长和∠CAO的度数；

（2）求点D的坐标；

（3）求过点A，O，D三点的抛物线的解析式；

（4）在（3）中，点P是抛物线上的一点，试确定点P的位置，使得△AOP的

面积与△AOC的面积相等.

 

 

 

 

 

 

 

 

 

 

 

 

Answer 1

（1）∵∠AOC=90^o，

∴AC是⊙O的直径，∴AC=2.

又∵点A的坐标为（-，0），∴OA=.

∴OC===1.

∴sin∠CAO==，∴∠CAO=30^o.………2分

（2）如图，连接OB，过点D作DE⊥x轴于点E.

∵OD为⊙O的切线，∴OB⊥OD，∴∠BOD=90^o.

∵AB=OB，∴∠AOB=∠OAB=30^o.

∴∠AOD=∠AOB+∠BOD=90^o +30^o=120^o.…………4分

在△AOD中，∠ODA=180^o-120^o -30^o=30^o=∠OAD，

∴OD=OA=.

在Rt△DOE中，∠DOE=180^o-120^o=60^o. ∴OE=OD·cos60^o=OD=，

ED=OD·sin60^o= . ∴点D的坐标为（，）……………………7分

（3）因为过点A，O，D三点的抛物线过原点，故设其解析式为y=ax²+bx.

将A(-，0)，D（，）代入解析式，得

      解得

∴过点A，O，D三点的抛物线解析式为y=x²+x..………………10分

（4）∵△AOP与△AOC面积相等，且有公共边OA，

∴OA边上的高相等

设P点的为（x，y），则=OC=1，y=±1.

当y=1时，x²+x=1，解方程得，x₁=，x₂=………………11分

当y=-1时，x²+x=-1，此方程△<0，方程无解.

∴当P点的坐标是（，1）或（，1）时，△AOP与△AOC面积相等.……………………………………………………………………………………12分

 

解析:略