题目内容
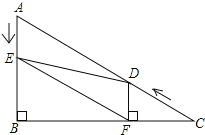
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上

(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=2,AC=2![]() ,点F是AD的中点,直接写出CF的长是 .
,点F是AD的中点,直接写出CF的长是 .
【答案】(1)见解析;(2)![]()
【解析】
(1)如图1(见解析),连接BD,先根据等腰直角三角形的性质得出![]() ,
,![]() ,再根据勾股定理可得出
,再根据勾股定理可得出![]() ,然后根据三角形全等的判定定理与性质可得
,然后根据三角形全等的判定定理与性质可得![]() ,
,![]() ,从而可得
,从而可得![]() ,最后在
,最后在![]() 中,利用勾股定理、等量代换即可得证;
中,利用勾股定理、等量代换即可得证;
(2)如图2(见解析),过点C作![]() 于H,先根据等腰三角形的性质、等腰直角三角形的性质得出
于H,先根据等腰三角形的性质、等腰直角三角形的性质得出![]() ,再根据题(1)的结论可求出
,再根据题(1)的结论可求出![]() ,从而可得DF的长,然后根据线段的和差、线段中点的定义可得
,从而可得DF的长,然后根据线段的和差、线段中点的定义可得![]() ,
,![]() ,最后利用勾股定理即可得.
,最后利用勾股定理即可得.
(1)如图1,连接BD
∵![]() 与
与![]() 都是等腰直角三角形
都是等腰直角三角形
∴![]() ,
,![]()
![]()
![]()
∴![]()
∵![]()
∴![]()
在![]() 和
和![]() 中,
中,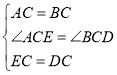
∴![]()
∴![]() ,
,![]()
∴![]()
在![]() 中,
中,![]()
∴![]() ;
;
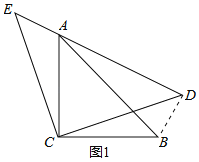
(2)如图2,过点C作![]() 于H
于H
则CH是DE边的中线(等腰三角形的三线合一)
![]()
由(1)可知,![]()
![]()
![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
![]()
![]()
∵点F是AD的中点
∴![]()
![]()
在![]() 中,
中,![]()
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目