题目内容
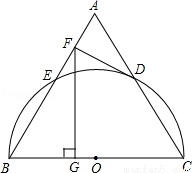
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
A.4
B.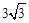 C.6
D.
C.6
D.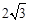
【答案】
B
【解析】
试题分析:连接OD,

∵DF为圆O的切线,∴OD⊥DF。
∵△ABC为等边三角形,∴AB=BC=AC,∠A=∠B=∠C=60°。
∵OD=OC,∴△OCD为等边三角形。∴OD∥AB。
又O为BC的中点,∴D为AC的中点,即OD为△ABC的中位线。
∴OD∥AB,∴DF⊥AB。
在Rt△AFD中,∠ADF=30°,AF=2,
∴AD=4,即AC=8。∴FB=AB﹣AF=8﹣2=6。
在Rt△BFG中,∠BFG=30°,∴BG=3。
则根据勾股定理得:FG= 。故选B。
。故选B。

练习册系列答案
相关题目
 BC,垂足为F
BC,垂足为F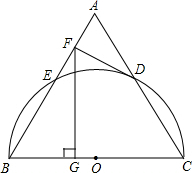 (2013•济宁)如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
(2013•济宁)如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )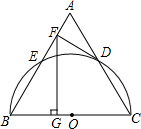 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为