题目内容
已知a、b、c是△ABC三边的长,则方程ax2+(b+c)x+ =0的根的情况为
=0的根的情况为
- A.没有实数根
- B.有两个相等的正实数根
- C.有两个不相等的负实数根
- D.有两个异号的实数根
C
分析:根据三角形的三边关系,确定出方程的根的判别式△的符号后,判断方程根的情况.
解答:∵a=a,b=(b+c),c=
∴△=b2-4ac=(b+c)2-4×a× =(b+c)2-a2=(a+b+c)(b+c-a)
=(b+c)2-a2=(a+b+c)(b+c-a)
∵三角形两边之和大于第三边,
∴a+b+c>0,b+c-a>0
∴△=(a+b+c)(b+c-a)>0
∴有两个不相等的实数根
根据一元二次方程根与系数的关系可得:两根的积是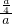 =
= >0,则两个根一定同号;
>0,则两个根一定同号;
两根的和是-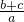 <0
<0
∴方程的两根都是负数.
故方程有两个不相等的负根.
故本题选C.
点评:总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
解决本题的关键是正确对(b+c)2-a2进行分解因式,能够结合一元二次方程的根与系数的关系判断方程根的符号.
分析:根据三角形的三边关系,确定出方程的根的判别式△的符号后,判断方程根的情况.
解答:∵a=a,b=(b+c),c=

∴△=b2-4ac=(b+c)2-4×a×
 =(b+c)2-a2=(a+b+c)(b+c-a)
=(b+c)2-a2=(a+b+c)(b+c-a)∵三角形两边之和大于第三边,
∴a+b+c>0,b+c-a>0
∴△=(a+b+c)(b+c-a)>0
∴有两个不相等的实数根
根据一元二次方程根与系数的关系可得:两根的积是
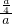 =
= >0,则两个根一定同号;
>0,则两个根一定同号;两根的和是-
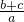 <0
<0∴方程的两根都是负数.
故方程有两个不相等的负根.
故本题选C.
点评:总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
解决本题的关键是正确对(b+c)2-a2进行分解因式,能够结合一元二次方程的根与系数的关系判断方程根的符号.

练习册系列答案
相关题目
 如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6. 米1.75元,建新围栏的价格是每米4.5元,设利用旧围栏CF的长度为x米,修建草坪围栏所需的总费用为y元.
米1.75元,建新围栏的价格是每米4.5元,设利用旧围栏CF的长度为x米,修建草坪围栏所需的总费用为y元.