题目内容
（2003•吉林）吉林省某大学的校门是一抛物线形水泥建筑物，大门的地面宽度为8米，两侧距P地面4米高处各有一个挂校名横匾用的铁环，两铁环的水平距离为6米，则校门的高为（精确到0.1米，水泥建筑物厚度忽略不计）（ ）
【答案】分析：假设抛物线方程为：y=ax2+bx+c根据图形，我们建立坐标轴，那么抛物线过：（-4 0）、（4 0）、（-3 4）、（3 4）这四个坐标．则利用这四个点坐标直接代到抛物线方程可以求c，而这个c刚好就是我们要求的那个高了．
解答：解：已知如图所示建立平面直角坐标系：
设抛物线的方程为y=ax2+bx+c，又已知抛物线经过（-4，0），（4，0），（-3，4），（3，4），
可得
，
求出a=-
，b=0，c=
，
故y=-
x2+
，
当x=0时，y≈9.1米．
故选B．
点评：本题考查点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．
解答：解：已知如图所示建立平面直角坐标系：
设抛物线的方程为y=ax2+bx+c，又已知抛物线经过（-4，0），（4，0），（-3，4），（3，4），
可得
，求出a=-
，b=0，c=，故y=-
x2+，当x=0时，y≈9.1米．
故选B．
点评：本题考查点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
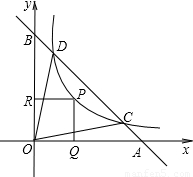
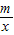的图象与AB交于C、D两点．P为双曲线y=
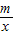上任一点，过P作PQ⊥x轴于Q，PR⊥y轴于R．请分别按（1）、（2）、（3）各自的要求解答问题．
