题目内容
5.设 A(1,y1),B(-2,y2),C(2,y3)是抛物线y=-(x+1)2+m上的三点,则y1、y2、y3的大小关系是( )| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y1>y3 |
分析 根据抛物线的性质,抛物线上的点离对称轴越远,对应的函数值就越小,由x取1、-2、2时,x取-2时所对应的点离对称轴最近,x取2时所对应的点离对称轴最远,即可得到答案.
解答 解:∵抛物线y=-(x+1)2+m开口向下,对称轴是直线x=-1,
∴抛物线上的点离对称轴越远,对应的函数值就越小,
∵x取2时所对应的点离对称轴最远,x取-2时所对应的点离对称轴近,
∴y2>y1>y3.
故选D.
点评 本题考查了二次函数图象上点的坐标特征.解题时,需熟悉抛物线的有关性质:抛物线的开口向下,则抛物线上的点离对称轴越远,对应的函数值就越小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在数轴上有一点M表示的数是3,而点N与点M的距离是2个单位长度,则点N所表示数是( )
| A. | -2 | B. | 1 | C. | 5 | D. | 1或5 |
20.若二次函数y=x2+bx的图象的对称轴是经过点(3,0)且平行于y轴的直线,则关于x的方程x2+bx=7的解为( )
| A. | x1=0,x2=6 | B. | x1=1,x2=7 | C. | x1=1,x2=-7 | D. | x1=-1,x2=7 |
10.不在直线y=-2x-3上的点是( )
| A. | (0,-3) | B. | (0.5,-4) | C. | (2,-7) | D. | (-1,-5) |
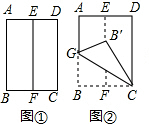 将长方形纸片ABCD按如下顺序进行折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③);请你求出图②中∠BCB′的度数.
将长方形纸片ABCD按如下顺序进行折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③);请你求出图②中∠BCB′的度数.