Question

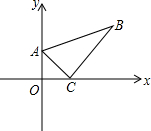如图，已知以点A（0，1）、C（1，0）为顶点的△ABC中，∠BAC=60°，∠ACB=90°，在坐标系内有一动点P，以P、B、C为顶点的三角形和△ABC全等，则P点坐标为

（0，1）、（2，-1）、(2+

3

，

3

-1)、(

3

，

3

+1)（答案无需化最简）

．

Answer 1

分析：求出AC，AB的值，根据题意得出符合的四种情况，画出图形，结合图形和全等三角形的性质求出每种情况即可．

解答：解：由勾股定理得：AC=

2

，
∵∠BAC=60°，∠ACB=90°，
∴AB=2

2

，BC=

6

，
分为四种情况：①当P和A重合时，△PCB≌△ACB，此时P的坐标是（0，1）；
②如图1，

延长AC到P，使AC=CP，连接BP，过P作PM⊥x轴于M，此时PM=OA=1，CM=OC=1，OM=1+1=2，
即P的坐标是（2，-1）；
③如图2，

过B作BP⊥BC，且BP=AC=

2

，此时PC=AB=2

2

过P作PM⊥x轴于M，此时∠PCM=15°，在x轴上取一点N，使∠PNM=30°，
即CN=PN，
设PM=x，则CN=PN=2x，MN=

3

x，
在Rt△CPM中，由勾股定理得：（2

2

）²=（2x+

3

x）²+x²，
x=

3

-1，
即PM=

3

-1，MC=2x+

3

x=

3

+1，
OM=1+

3

+1=2+

3

，
即P的坐标是（2+

3

，

3

-1）；
④如图3，

过B作BP⊥BC，且BP=AC=

2

，过P作PM⊥x轴于M，
此时∠PCM=30°+45°=75°，∠CPM=15°，和③解法类似求出CM=

3

-1，
PM=2x+

3

x=

3

+1，OM=1+

3

-1=

3

，
即P的坐标是（

3

，

3

+1），
故答案为：（0，1）或（2，-1）或（2+

3

，

3

-1）或（

3

，

3

+1）．

点评：本题考查了全等三角形的性质和判定，勾股定理，含30度角的直角三角形等知识点的应用，注意要进行分类讨论，题目比较好，但是有一定的难度．