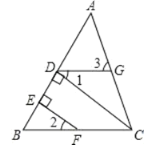
ĢāÄæÄŚČŻ
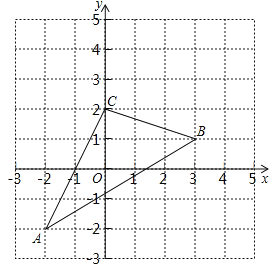
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćC£Ø©3£¬0£©£¬µćA£¬B·Ö±šŌŚxÖį£¬yÖįµÄÕż°ėÖįÉĻ£¬ĒŅĀś×ć ![]() +|OA©1|=0
+|OA©1|=0
£Ø1£©ĒóµćA£¬µćBµÄ×ų±ź£®
£Ø2£©ČōµćP“ÓCµć³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲÉäĻßCBŌĖ¶Æ£¬Į¬½įAP£®Éč”÷ABPµÄĆ껿ĪŖS£¬µćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬ĒóSÓėtµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮæµÄȔֵ·¶Ī§£®
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ŹĒ·ń“ęŌŚµćP£¬Ź¹ŅŌµćA£¬B£¬PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AOBĻąĖĘ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ
£Ø1£©½ā£ŗ”ß ![]() +|OA©1|=0
+|OA©1|=0
”ąOA©1=0”¢OB2©3=0£¬
”ąOA=1”¢OB= ![]() £¬
£¬
”ąµćAµÄ×ų±źĪŖ£Ø1£¬0£©”¢BµÄ×ų±ź£Ø0£¬ ![]() £©
£©

£Ø2£©½ā£ŗ”ßC£Ø©3£¬0£©£¬B£Ø0£¬ ![]() £©£»
£©£»
”ąOC=3£¬OB= ![]()
ŌŚRT”÷BOCÖŠ£¬BC= ![]() =2
=2 ![]() £¬
£¬
ÉčµćAµ½Ö±ĻßCBµÄ¾ąĄėĪŖy£¬Ōņ
![]() ”Į2
”Į2 ![]() y=
y= ![]() ”Į£Ø3+1£©”Į
”Į£Ø3+1£©”Į ![]() £¬
£¬
½āµĆy=2£®
ŌņS= ![]() ”Į|2
”Į|2 ![]() ©t|”Į2=|2
©t|”Į2=|2 ![]() ©t|£®
©t|£®
¹ŹSÓėtµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗS=©t+2 ![]() £Ø0”Üt”Ü2
£Ø0”Üt”Ü2 ![]() £©»ņS=t©2
£©»ņS=t©2 ![]() £Øt£¾2
£Øt£¾2 ![]() £©£®
£©£®
£Ø3£©½ā£ŗ“ęŌŚ£¬
ĄķÓÉ£ŗ”ßtan”ĻOBC= ![]() =
= ![]() =
= ![]() £¬
£¬
”ą”ĻOBC=60”ć£¬
”ą”ĻBCO=30”ć£¬
”ąBC=2OB=2 ![]() £¬
£¬
”ßtan”ĻOBA= ![]() =
= ![]() =
= ![]() £¬
£¬
”ą”ĻOBA=30”ć£¬
”ą”ĻABC=90”ć£¬AB=2OA=2£¬
¢Łµ±0”Üt”Ü2 ![]() Ź±£¬Čō”÷PBA”×”÷AOBŹ±£¬Ōņ
Ź±£¬Čō”÷PBA”×”÷AOBŹ±£¬Ōņ ![]() =
= ![]() £¬
£¬
¼“ ![]() =
= ![]() £¬
£¬
”ąPB= ![]() £¬
£¬
”ąPBsin60”ć= ![]() ”Į
”Į ![]() =1£¬PBcos60”ć=
=1£¬PBcos60”ć= ![]() ”Į
”Į ![]() =
= ![]() £¬
£¬
”ąP£Ø©1£¬ ![]() £©£»
£©£»
Čō”÷ABP”×”÷AOBŹ±£¬Ōņ ![]() =
= ![]() £¬
£¬
¼“ ![]() =
= ![]() £¬
£¬
”ąPB=2 ![]() £¬
£¬
”ąPBsin60”ć=2 ![]() ”Į
”Į ![]() =3£¬PBcos60”ć=2
=3£¬PBcos60”ć=2 ![]() ”Į
”Į ![]() =
= ![]() £¬
£¬
”ąP£Ø©3£¬0£©£¬
¢Śµ±t£¾2 ![]() Ź±£¬Čō”÷PBA”×”÷AOBŹ±£¬Ōņ
Ź±£¬Čō”÷PBA”×”÷AOBŹ±£¬Ōņ ![]() =
= ![]() £¬
£¬
¼“ ![]() =
= ![]() £¬
£¬
”ąPB= ![]() £¬
£¬
”ąPBsin60”ć= ![]() ”Į
”Į ![]() =1£¬PBcos60”ć=
=1£¬PBcos60”ć= ![]() ”Į
”Į ![]() =
= ![]() £¬
£¬
”ąP£Ø1£¬ ![]() £©£»
£©£»
Čō”÷ABP”×”÷AOBŹ±£¬Ōņ ![]() =
= ![]() £¬
£¬
¼“ ![]() =
= ![]() £¬
£¬
”ąPB=2 ![]() £¬
£¬
”ąPBsin60”ć=2 ![]() ”Į
”Į ![]() =3£¬PBcos60”ć=2
=3£¬PBcos60”ć=2 ![]() ”Į
”Į ![]() =
= ![]() £¬
£¬
”ąP£Ø3£¬2 ![]() £©£¬
£©£¬
ĖłŅŌ£¬“ęŌŚµćP£¬Ź¹ŅŌµćA£¬B£¬PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AOBĻąĖĘ£¬PµćµÄ×ų±źĪŖ£Ø©1£¬ ![]() £©»ņ£Ø©3£¬0£©»ņ£Ø1£¬
£©»ņ£Ø©3£¬0£©»ņ£Ø1£¬ ![]() £©»ņ£Ø3£¬2
£©»ņ£Ø3£¬2 ![]() £©£®
£©£®
”¾½āĪö”æ£Ø1£©øł¾Ż·ĒøŗŹżµÄŗĶĪŖ0£¬ĆæøöŹż¾łĪŖ0£¬µĆµ½OA”¢OBµÄ³¤£¬¼“æÉĒó³ö“š°ø£»£Ø2£©øł¾Ż¹“¹É¶ØĄķµĆµ½CBµÄ³¤¶Č£¬ŌŁøł¾ŻČż½ĒŠĪĆ껿¹«Ź½¼“æɵƵ½µćAµ½Ö±ĻßCBµÄ¾ąĄė£»ŌŁøł¾Ż”÷ABPµÄĆ껿=![]() BP
BP![]() AB£¬ÓĆtµÄ“śŹżŹ½±ķŹ¾BP¼“|
AB£¬ÓĆtµÄ“śŹżŹ½±ķŹ¾BP¼“|![]() ©t|£¬¼“æɵƵ½SÓėtµÄŗÆŹż¹ŲĻµŹ½ÓÉÓŚŹĒÉäĻßCB£¬æÉ·ÖĪŖPŌŚĻ߶ĪCBÉĻŗĶŌŚCBŃÓ³¤ĻßÉĻĮ½ÖÖĒéæö£»£Ø3£©ĻČĒóµĆ”ĻABC=90”ć£¬Č»ŗó·ÖĮ½ÖÖĒéæöĢÖĀŪ£ŗ¢Łµ±0”Üt”Ü
©t|£¬¼“æɵƵ½SÓėtµÄŗÆŹż¹ŲĻµŹ½ÓÉÓŚŹĒÉäĻßCB£¬æÉ·ÖĪŖPŌŚĻ߶ĪCBÉĻŗĶŌŚCBŃÓ³¤ĻßÉĻĮ½ÖÖĒéæö£»£Ø3£©ĻČĒóµĆ”ĻABC=90”ć£¬Č»ŗó·ÖĮ½ÖÖĒéæöĢÖĀŪ£ŗ¢Łµ±0”Üt”Ü![]() ¢Śµ±t£¾
¢Śµ±t£¾![]() , ĄūÓƶŌÓ¦±ß³É±ČĄżĮŠ³ö·½³Ģ£¬ŌŁŌĖÓĆČż½ĒŗÆŹż£¬¼“æÉĒóµĆµćPµÄ×ų±ź£®
, ĄūÓƶŌÓ¦±ß³É±ČĄżĮŠ³ö·½³Ģ£¬ŌŁŌĖÓĆČż½ĒŗÆŹż£¬¼“æÉĒóµĆµćPµÄ×ų±ź£®
”¾æ¼µć¾«Īö”æ¹ŲÓŚ±¾Ģāæ¼²éµÄČż½ĒŠĪµÄĆ껿ŗĶ¹“¹É¶ØĄķµÄøÅÄī£¬ŠčŅŖĮĖ½āČż½ĒŠĪµÄĆ껿=1/2”Įµ×”Įøߣ»Ö±½ĒČż½ĒŠĪĮ½Ö±½Ē±ßa”¢bµÄĘ½·½ŗĶµČÓŚŠ±±ßcµÄĘ½·½,¼“;a2+b2=c2²ÅÄÜµĆ³öÕżČ·“š°ø£®

 Ļ°Ģā¾«Ń”ĻµĮŠ“š°ø
Ļ°Ģā¾«Ń”ĻµĮŠ“š°ø”¾ĢāÄæ”æA£¬B£¬CČżĆū“óѧɜ¾ŗŃ”ĻµŃ§Éś»įÖ÷ĻÆ£¬ĖūĆĒµÄ±ŹŹŌ³É¼ØŗĶæŚŹŌ³É¼Ø£Øµ„Ī»£ŗ·Ö£©·Ö±šÓĆĮĖĮ½ÖÖ·½Ź½½ųŠŠĮĖĶ³¼Ę£¬Čē±ķŗĶĶ¼Ņ»£ŗ
A | B | C | |
±ŹŹŌ | 85 | 95 | 90 |
æŚŹŌ | 80 | 85 |
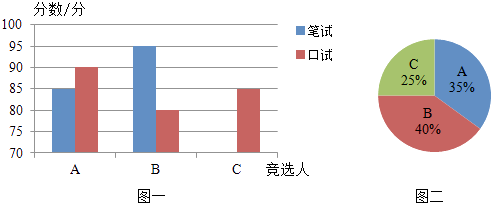
£Ø1£©Ēė½«±ķŅ»ŗĶĶ¼Ņ»ÖŠµÄæÕȱ²æ·Ö²¹³äĶźÕū£®
£Ø2£©¾ŗŃ”µÄ×īŗóŅ»øö³ĢŠņŹĒÓɱ¾ĻµµÄ300Ćūѧɜ½ųŠŠĶ¶Ę±£¬ČżĪ»ŗņŃ”ČĖµÄµĆʱĒéæöČēĶ¼¶ž£ØƻӊʜČØʱ£¬ĆæĆūѧɜֻÄÜĶĘ¼öŅ»øö£©£¬Ēė¼ĘĖćĆæČĖµÄµĆʱŹż£®
£Ø3£©ČōĆæʱ¼Ę1·Ö£¬ĻµĄļ½«±ŹŹŌ”¢æŚŹŌ”¢µĆʱȿĻī²āŹŌµĆ·Ö°“4£ŗ3£ŗ3µÄ±ČĄżČ·¶ØøöČĖ³É¼Ø£¬Ēė¼ĘĖćČżĪ»ŗņŃ”ČĖµÄ×īŗó³É¼Ø£¬²¢øł¾Ż³É¼ØÅŠ¶ĻĖÄܵ±Ń”£®