题目内容
如图,在 中,
中, ,
, ,
, ,AF=10cm, AC=14cm,动点E以2cm/s的速度从
,AF=10cm, AC=14cm,动点E以2cm/s的速度从 点向
点向 点运动,动点
点运动,动点 以1cm/s的速度从
以1cm/s的速度从 点向
点向 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t
点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t

(1)求证:在运动过程中,不管t取何值,都有 ;
;
(2)当t取何值时, 与
与 全等
全等
【答案】
(1) 详见解析; (2)

【解析】
试题分析:(1)利用角平分线上的点到角两边的距离相等可以得到DF=DM,再利用三角形的面积公式表示出两个三角形的面积即可证得结论
(2)若两个三角形全等,那么可以得到EF=MG EF=10-2t,AM=AF=10,CM=14-10=4,此时要分两种情况,点G在CM上运动或在MA上运动,分别表示出MG的长,解出t的值即可 要注意检验t的值是否符合题意
试题解析:(1)

 (4分)
(4分)
(2)

 ,
, ,
,

当 时,
时, ,所以
,所以 舍去 (6分)
舍去 (6分)
 ,
,

综上所述,当 时,
时, 与
与 全等 (8分)
全等 (8分)
考点:1 全等三角形的性质;2 三角形的面积公式

练习册系列答案
相关题目
 中,
中, 是
是 边上的高,
边上的高, 是
是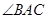 平分线。求
平分线。求 的度数。
的度数。
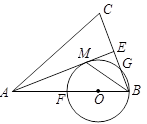
 中,
中, ,
, 平分
平分 交
交 于
于 ,点
,点 在
在 上,以
上,以 为半径的圆,交
为半径的圆,交 ,交
,交 于
于 ,且点
,且点 ,切⊙
,切⊙


 ,求⊙
,求⊙ 中,
中, D是BC上的点,
D是BC上的点,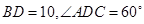 .求AC(
.求AC(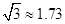 ,结果保留整数).
,结果保留整数).
 中,
中, ,点
,点 在
在 上,以
上,以 长为半径的圆与
长为半径的圆与 分别交于点
分别交于点 ,且
,且 .
. 与
与 的位置关系,并证明你的结论;
的位置关系,并证明你的结论; ,
, ,求
,求 的值.
的值.