Question

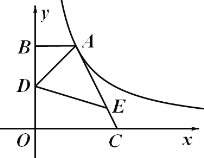
【题目】在平面直角坐标系中，点在轴的正半轴上，点在轴正半轴上，且，满足等式．点从点出发，沿轴的正半轴运动，过点作轴的垂线，是垂线在第一象限内的一动点，且．

（1）求，的值；

（2）若点在线段上，当时，求点的坐标；

（3）若点在线段的延长线上，的垂直平分线交轴于点，并且恰好经过点，求此时的面积．

Answer 1

【答案】（1），；（2）；（3）56

【解析】

（1）根据偶次幂和绝对值的非负性即可得；

（2）先根据直角三角形的性质得出，再根据三角形全等的判定定理与性质可得，然后根据线段的和差可得的长，从而可得点P坐标；

（3）如图2（见解析），先根据垂直平分线的性质、直角三角形全等的判定定理与性质得出，再根据等腰三角形的性质、平行线的判定得出，然后根据等腰直角三角形的判定与性质得出，从而可得MB的长，最后根据三角形的面积公式即可得．

（1）

，

解得：，；

（2）如图1，，轴

在和中，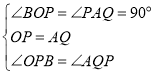

由（1）可知：

则点P的坐标为；

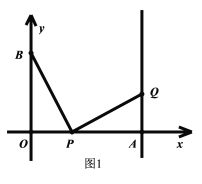
（3）如图2，设交于点，连接

是BQ的垂直平分线

在和中，

，，

，即

（等腰三角形的三线合一）

是等腰直角三角形，且

即此时的面积为56．