题目内容
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点G、H在线段DE上,且DG=GH=HE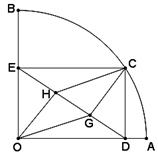
(1)求证:四边形OGCH是平行四边形;
(2)当点C在弧AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;
(3)求证: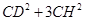 是定值.
是定值.
(1)连结OC,交DE于M,
∵四边形ODCE是矩形
∴OM=CM,EM=DM
又∵DG=HE
∴EM-EH=DM-DG,即HM=GM
∴四边形OGCH是平行四边形
(2)DG不变;
在矩形ODCE中,DE=OC=3,所以DG=1
(3)作HF⊥CD于点F,则△DHF∽△DEC
∴
∴
∴
∵HF2=CH2-CF2=DH2-DF2,DH=2
∴CH2- =2-
=2-
整理,得
∴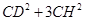 ="12"
="12"
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是
是
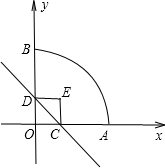
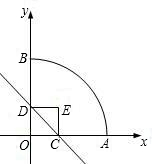 标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则: 是______;
是______; 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积. 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.
 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.