题目内容
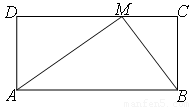
若从矩形一边上的点到对边的视角是直角,则称该点为直角点.例如,如图的矩形ABC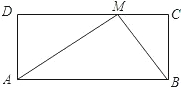 D中,点M在CD边上,连AM,BM,∠AMB=90°,则点M为直角点.
D中,点M在CD边上,连AM,BM,∠AMB=90°,则点M为直角点.(1)若矩形ABCD一边CD上的直角点M为中点,问该矩形的邻边具有何种数量关系?并说明理由;
(2)若点M,N分别为矩形ABCD边CD,AB上的直角点,且AB=4,BC=
| 3 |
分析:(1)根据已知条件即可证明三角形ADM是等腰直角三角形,则该矩形的长是宽的2倍;
(2)作MH⊥AB于点H,能够据一已知条件求得构造的直角三角形的两条直角边.
(2)作MH⊥AB于点H,能够据一已知条件求得构造的直角三角形的两条直角边.
解答: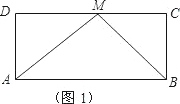 解:(1)AB=2AD.
解:(1)AB=2AD.
理由如下:
∵直角点M为CD边的中点,
∴MD=MC,
又∵AD=BC,∠D=∠C=90°
∴△ADM≌△BCM,
∴∠AMD=∠BMC,
∵∠AMB=90°,
∴∠AMD+∠BMC=90°,
∴∠AMD=∠BMC=45°
∴∠DAM=∠AMD=45°,
∴AD=DM,
∴AB=2AD.
(2)如图2所示,作MH⊥AB于点H,连接MN
∵∠AMB=90°,
∴∠AMD+∠BMC=90°,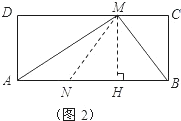
∵∠AMD+∠DAM=90°,
∴∠DAM=∠BMC
又∵∠D=∠C,
∴△ADM∽△MCB,
∴
=
,即
=
,
∴MC=1或3.
∵点M,N分别为矩形ABCD边CD,AB上的直角点,
∴AN=MC,
∴当MC=1时,AN=1,NH=2,
∴MN2=MH2+NH2=(
)2+22=7,
∴MN=
.
当MC=3时,此时点N与点H重合,即MN=BC=
,
综上,MN=
或
.
 解:(1)AB=2AD.
解:(1)AB=2AD.理由如下:
∵直角点M为CD边的中点,
∴MD=MC,
又∵AD=BC,∠D=∠C=90°
∴△ADM≌△BCM,
∴∠AMD=∠BMC,
∵∠AMB=90°,
∴∠AMD+∠BMC=90°,
∴∠AMD=∠BMC=45°
∴∠DAM=∠AMD=45°,
∴AD=DM,
∴AB=2AD.
(2)如图2所示,作MH⊥AB于点H,连接MN
∵∠AMB=90°,
∴∠AMD+∠BMC=90°,

∵∠AMD+∠DAM=90°,
∴∠DAM=∠BMC
又∵∠D=∠C,
∴△ADM∽△MCB,
∴
| AD |
| MC |
| DM |
| BC |
| ||
| MC |
| 4-MC | ||
|
∴MC=1或3.
∵点M,N分别为矩形ABCD边CD,AB上的直角点,
∴AN=MC,
∴当MC=1时,AN=1,NH=2,
∴MN2=MH2+NH2=(
| 3 |
∴MN=
| 7 |
当MC=3时,此时点N与点H重合,即MN=BC=
| 3 |
综上,MN=
| 7 |
| 3 |
点评:熟练运用勾股定理、全等三角形的判定、相似三角形的判定进行计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 若从矩形一边上的点到对边的视角是直角,即称该点是直角点.例如,如图的矩形ABCD中,点M在CD边上,连接AM、BM,∠AMB=90°,则点M为直角点.若点M、N分别为矩形ABCD的边CD、AB上的直角点,且AB=4,BC=
若从矩形一边上的点到对边的视角是直角,即称该点是直角点.例如,如图的矩形ABCD中,点M在CD边上,连接AM、BM,∠AMB=90°,则点M为直角点.若点M、N分别为矩形ABCD的边CD、AB上的直角点,且AB=4,BC=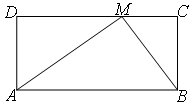
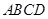 中,点
中,点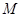 在
在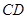 边上,连接
边上,连接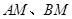 ,
,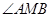
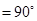 ,则点
,则点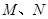 分别为矩形
分别为矩形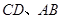 上的直角点,且
上的直角点,且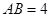 ,
,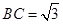 ,则
,则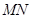 的长为
的长为 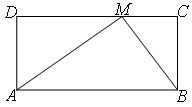
 中,点
中,点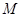 在
在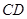 边上,连接
边上,连接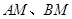 ,
,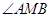
 ,则点
,则点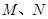 分别为矩形
分别为矩形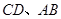 上的直角点,且
上的直角点,且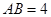 ,
,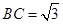 ,则
,则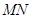 的长为
的长为