题目内容
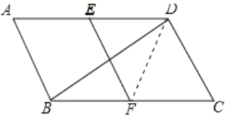
【题目】如图，在平行四边形
中，
，
，
分别是
，
的中点，
．
（1）求证：四边形
是菱形；
（2）求
的长．
【答案】（1）见解析；（2）
【解析】
（1）由平行四边形的性质得出AD∥BC，AD＝BC，证出DE∥CF，DE＝CF，得出四边形CDEF是平行四边形，证出CD＝CF，即可得出四边形CDEF是菱形；
（2）连接DF，证明△CDF是等边三角形，得出∠CDF＝∠CFD＝60°，求出∠BDF＝30°，证出∠BDC＝∠BDF＋∠CDF＝90°，由勾股定理即可得出答案．
（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∵E，F分别是AD，BC的中点，
∴DE＝
AD，CF＝BC，
∴DE∥CF，DE＝CF，
∴四边形CDEF是平行四边形，
又∵BC＝2CD，
∴CD＝CF，
∴四边形CDEF是菱形；
（2）如图，连接
，
，
，
是等边三角形，
，
，
．
是
的中点，
，
．
，
．
，
．
练习册系列答案
阅读快车系列答案
相关题目
