题目内容
古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”(如图①),而把1,4,9,16,…这样的数称为“正方形数”(如图②). 如果规定a1=1,a2=3,a3=6,a4=10,…;b1=1,b2=4,b3=9,b4=16,…;y1=2a1+b1,y2=2a2+b2,y3=2a3+b3,y4=2a4+b4,…,那么,按此规定,y6=( )
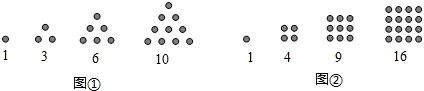
A.78 B.72 C.66 D.56
A【考点】规律型:图形的变化类;规律型:数字的变化类.
【分析】根据题中给出的数据可得a6=1+2+3+…+6,b6=62,把相关数值代入y6的代数式计算即可.
【解答】解:∵a1=1,a2=1+2=3,a3=1+2+3=6,a4=1+2+3+4=10,…;
b1=12,b2=22=4,b3=32=9,b4=42=16,
∴a6=1+2+3+…+6,b6=62,
∴y6=2a6+b6=2×21+36=78.
故选A.
【点评】本题考查图形的变化规律,根据题意得出得到an,bn的计算方法是解决本题的关键.

练习册系列答案
相关题目
(8分)用火柴棒按下列方式搭建三角形:

(1)填表:
| 三角形个数/个 | 1 | 2 | 3 | 4 | … |
| 火柴棒根数/根 | 3 | 5 |
(2) 当三角形的个数为n时,火柴棒的根数是多少?
(3)求当n=1004时,火柴棒的根数是多少?

 是一次二项式,(4)3a2-4a+1的项是3a2,4a,1
是一次二项式,(4)3a2-4a+1的项是3a2,4a,1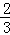 __________﹣
__________﹣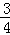 .
.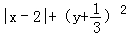 =0,则yx的值是__________.
=0,则yx的值是__________. m+n,﹣
m+n,﹣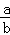 ,0,
,0,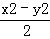 中,单项式有( )
中,单项式有( )