题目内容
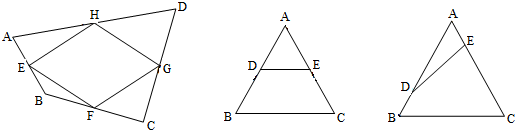
顺次连接四边形ABCD的四条边的中点,得到一个矩形,那么
- A.AC=BD
- B.AC⊥BD
- C.AB=CD
- D.AB⊥CD
B
分析:根据矩形的性质得到∠FEH=90°,根据三角形的中位线定理得出EF∥AC,根据平行线的性质推出∠FEH+∠CME=180°,∠EMC+∠BOA=180°,即推出∠BOA=∠FEH=90°,即可得到答案.
解答: 解:∵矩形EFGH,
解:∵矩形EFGH,
∴∠FEH=90°,
∵E是AB的中点,F是BC的中点,
∴EF∥AC,
∴∠FEH+∠CME=180°,
同理EH∥BD,
∴∠EMC+∠BOA=180°,
∴∠BOA=∠FEH=90°,
∴AC⊥BD,
故选B.
点评:本题主要考查对矩形的性质和判定,三角形的中位线定理,平行线的性质,垂直的定义等知识点的理解和掌握,能灵活运用这些性质进行证明是证此题的关键.题型较好,难度适中.
分析:根据矩形的性质得到∠FEH=90°,根据三角形的中位线定理得出EF∥AC,根据平行线的性质推出∠FEH+∠CME=180°,∠EMC+∠BOA=180°,即推出∠BOA=∠FEH=90°,即可得到答案.
解答:
 解:∵矩形EFGH,
解:∵矩形EFGH,∴∠FEH=90°,
∵E是AB的中点,F是BC的中点,
∴EF∥AC,
∴∠FEH+∠CME=180°,
同理EH∥BD,
∴∠EMC+∠BOA=180°,
∴∠BOA=∠FEH=90°,
∴AC⊥BD,
故选B.
点评:本题主要考查对矩形的性质和判定,三角形的中位线定理,平行线的性质,垂直的定义等知识点的理解和掌握,能灵活运用这些性质进行证明是证此题的关键.题型较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=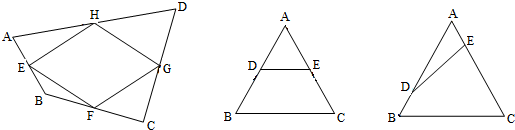
 如图,在边长为1的正方形网格中,△A′B′C′与△ABC是中心对称图形.
如图,在边长为1的正方形网格中,△A′B′C′与△ABC是中心对称图形.