Question

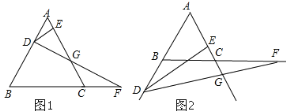
【题目】在△ABC中，AB=10，CA=8，BC=6，∠BAC的平分线与∠BCA的平分线交于点I，且DI∥BC交AB于点D,则DI的长为____.

Answer 1

【答案】2.5

【解析】

根据题意，△ABC是直角三角形，延长DI交AC于点E，过I作IF⊥AB，IG⊥BC，由点I是内心，则，利用等面积的方法求得，然后利用平行线分线段成比例，得，又由BD=DI，把数据代入计算，即可得到DI的长度.

解：如图，延长DI交AC于点E，过I作IF⊥AB，IG⊥BC，

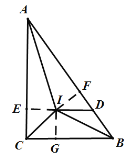
在△ABC中，AB=10，CA=8，BC=6，

∴，

∴△ABC是直角三角形，即AC⊥BC，

∵DI∥BC，

∴DE⊥AC，

∵∠BAC的平分线与∠BCA的平分线交于点I，

∴点I是三角形的内心，则，

在△ABC中，根据等面积的方法，有

，设

即，

解得：，

∵DI∥BC，

∴，∠DIB=∠CBI=∠DBI，

∴DI=BD，

∴，

解得：BD=2.5，

∴DI=2.5；

故答案为：2.5.