题目内容
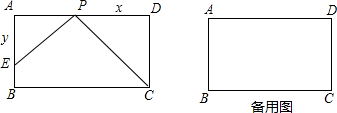
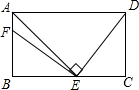 已知矩形ABCD中,AB=4,BC=7.∠BAD的平分线AE交BC于E点,EF⊥DE交AB于F点,则EF的长为________.
已知矩形ABCD中,AB=4,BC=7.∠BAD的平分线AE交BC于E点,EF⊥DE交AB于F点,则EF的长为________.
5
分析:由角平分线可得BE的长,进而得出CE、DE的长,再在直角三角形中由勾股定理求解AF的长,即可得出结论.
解答: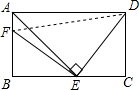 解:连接DF,
解:连接DF,
在矩形ABCD中,∵AE平分∠BAD,
∴BE=AB=4,CE=BC-BE=7-4=3,
则在Rt△CDE中,DE=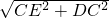 =5,
=5,
在Rt△AFD中,AF2+AD2=DF2,
即AF2+72=DF2,①
在Rt△BEF中,(4-AF)2+42=EF2,②
在Rt△EFD中,DF2=EF2+52,③
化简可得AF2=1,即AF=1,
∴BF=3,
则在Rt△BEF中,EF= =5.
=5.
故答案为:5.
点评:本题主要考查了角平分线的性质以及勾股定理的运用,能够熟练运用勾股定理求解一些简单的直角三角形的计算问题.
分析:由角平分线可得BE的长,进而得出CE、DE的长,再在直角三角形中由勾股定理求解AF的长,即可得出结论.
解答:
 解:连接DF,
解:连接DF,在矩形ABCD中,∵AE平分∠BAD,
∴BE=AB=4,CE=BC-BE=7-4=3,
则在Rt△CDE中,DE=
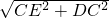 =5,
=5,在Rt△AFD中,AF2+AD2=DF2,
即AF2+72=DF2,①
在Rt△BEF中,(4-AF)2+42=EF2,②
在Rt△EFD中,DF2=EF2+52,③
化简可得AF2=1,即AF=1,
∴BF=3,
则在Rt△BEF中,EF=
 =5.
=5.故答案为:5.
点评:本题主要考查了角平分线的性质以及勾股定理的运用,能够熟练运用勾股定理求解一些简单的直角三角形的计算问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
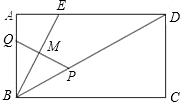 ,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S.
,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S. 如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P.
如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P. 如图:已知矩形ABCD中,CE∥DF.
如图:已知矩形ABCD中,CE∥DF.