题目内容
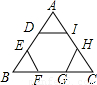
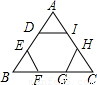
 如图,正六边形ABCDEF中,P是ED上一点,直线DC与射线AP,AB相交于M,N.当△AMN面积与正六边形ABCDEF面积相等时,
如图,正六边形ABCDEF中,P是ED上一点,直线DC与射线AP,AB相交于M,N.当△AMN面积与正六边形ABCDEF面积相等时,| EP | PD |
分析:先连接AE,过F作FG⊥AE于G,由等腰三角形的性质及锐角三角函数的定义可求出AE的长,再设正六边形ABCDEF的边长为a,△NPD的高为h,根据ED∥AM可知△NED∽△NAM,再根据正六边形内角的度数可得出△BMC是等边三角形,即AM=2a,再由△AMN面积与正六边形ABCDEF面积相等即可求出h的值,再根据相似三角形的对应边成比例即可求解.
解答: 解:先连接AE,过F作FG⊥AE于G,
解:先连接AE,过F作FG⊥AE于G,
∵六边形ABCDEF是正六边形,设正六边形ABCDEF的边长为a,△NPD的高为h,
∴AE=2EG=2×EF×cos∠AEF=2×a×
=
a,
S正六边形ABCDEF=6×
a×
=
,
∵∠ABC=∠BCD=120°,
∴∠CBM=∠BCM=60°,
∴△BMC是等边三角形,
∴BM=a,
∵△AMN面积与正六边形ABCDEF面积,
∴S△AMN=
AM•(AE+h)=
×2a(
a+h)=
,
∴h=
,
∵ED∥AB,
∴△NPD∽△NAM,
∴
=
,即
=
,
解得PD=
,
∴PE=
a,
∴
=
.
故答案为:
.
 解:先连接AE,过F作FG⊥AE于G,
解:先连接AE,过F作FG⊥AE于G,∵六边形ABCDEF是正六边形,设正六边形ABCDEF的边长为a,△NPD的高为h,
∴AE=2EG=2×EF×cos∠AEF=2×a×
| ||
| 2 |
| 3 |
S正六边形ABCDEF=6×
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∵∠ABC=∠BCD=120°,
∴∠CBM=∠BCM=60°,
∴△BMC是等边三角形,
∴BM=a,
∵△AMN面积与正六边形ABCDEF面积,
∴S△AMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
∴h=
| ||
| 2 |
∵ED∥AB,
∴△NPD∽△NAM,
∴
| PD |
| AM |
| h | ||
h+
|
| PD |
| 2a |
| ||||||
|
解得PD=
| 2a |
| 3 |
∴PE=
| 1 |
| 3 |
∴
| EP |
| PD |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的是面积及等积变换,熟知正六边形的性质及相似三角形的判定与性质是解答此题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
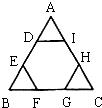 18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是
18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是