题目内容
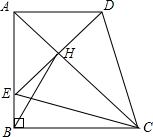 在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交对角线AC于H,连接BH.下列结论:
在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交对角线AC于H,连接BH.下列结论:①△ACD≌△ACE;②△CDE为等边三角形;③
| EH |
| BE |
| S△EBC |
| S△EHC |
| AH |
| CH |
其中结论正确的是
分析:△AED与△ABC是等腰直角三角形,根据这个条件就可求得:△ACD≌△ACE的条件,就可进行判断.
解答:解:∵∠ABC=90°,AB=BC
∴∠BAC=∠ACB=45°
又∵∠BAD=90°
∴∠BAC=∠DAC
又AD=AE,AC=AC
∴①△ACD≌△ACE;故①正确;
同理∠AED=45°
∠BEC=90°-∠BCE=90°-15°=75°
∴∠DEC=60°
∵ACD≌△ACE
∴CD=CE
∴②△CDE为等边三角形.故②正确.
③∵△CHE为直角三角形,且∠HEC=60°
∴EC=2EH
∵∠ECB=15°,
∴EC≠4EB,
∴
=2不成立;
④作EC的中垂线交BC于点F,连接EF,则EF=FC,
∴∠FEC=∠BCE=15°,
∴∠BFE=30°,
设BE=a,
则EF=FC=2a,
在直角△BEF中,BF=
a,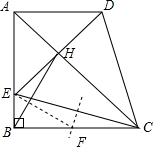
∴BC=
a+2a=(2+
)a,
∴S△BEC=
BE•BC=
a2;
在直角△BEC中,EC=
=2
a,
∵△CDE为等边三角形,
∴S△ECD=
=
(2+
)=(3+2
)a2,EH=
a,HC=
EC=
a,
又∵△AED是等腰直角三角形,AH是高,
∴AH=EH=
a,
∴S△EHC=
a2,
∴
=
=
=
=
.故④正确;
故其中结论正确的是①②④.
∴∠BAC=∠ACB=45°
又∵∠BAD=90°
∴∠BAC=∠DAC
又AD=AE,AC=AC
∴①△ACD≌△ACE;故①正确;
同理∠AED=45°
∠BEC=90°-∠BCE=90°-15°=75°
∴∠DEC=60°
∵ACD≌△ACE
∴CD=CE
∴②△CDE为等边三角形.故②正确.
③∵△CHE为直角三角形,且∠HEC=60°
∴EC=2EH
∵∠ECB=15°,
∴EC≠4EB,
∴
| EH |
| BE |
④作EC的中垂线交BC于点F,连接EF,则EF=FC,
∴∠FEC=∠BCE=15°,
∴∠BFE=30°,
设BE=a,
则EF=FC=2a,
在直角△BEF中,BF=
| 3 |

∴BC=
| 3 |
| 3 |
∴S△BEC=
| 1 |
| 2 |
| ||
| 2 |
在直角△BEC中,EC=
| BE2+BC2 |
2+
|
∵△CDE为等边三角形,
∴S△ECD=
| ||
| 4 |
| 3 |
| 3 |
| 3 |
2+
|
| ||
| 2 |
3+2
|
又∵△AED是等腰直角三角形,AH是高,
∴AH=EH=
2+
|
∴S△EHC=
3+2
| ||
| 2 |
∴
| S△EBC |
| S△EHC |
| ||||
|
| ||
3+2
|
| ||||
|
| AH |
| CH |
故其中结论正确的是①②④.
点评:认识到题目中的等腰直角三角形是解决本题的关键.

练习册系列答案
相关题目
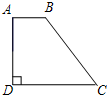 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
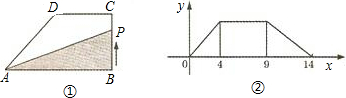
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )