题目内容
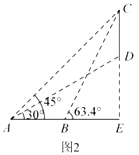
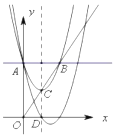
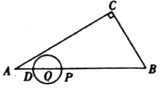
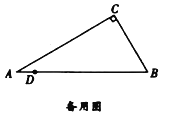
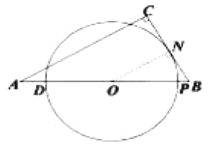
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() .点
.点![]() 从
从![]() 点出发,沿
点出发,沿![]() 方向运动,以
方向运动,以![]() 为直径作
为直径作![]() ,当
,当![]() 运动到点
运动到点![]() 时停止运动,设
时停止运动,设![]() .
.
(1)![]() ___________,
___________,![]() ___________.(用
___________.(用![]() 的代数式表示)
的代数式表示)
(2)当![]() 为何值时,
为何值时,![]() 与
与![]() 的一边相切?
的一边相切?
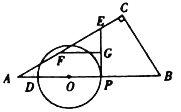
(3)在点![]() 整个运动过程中,过点
整个运动过程中,过点![]() 作
作![]() 的切线交折线
的切线交折线![]() 于点
于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,过
,过![]() 作
作![]() 于
于![]() .
.

①当线段![]() 长度达到最大时,求
长度达到最大时,求![]() 的值;
的值;
②直接写出点![]() 所经过的路径长是________.(结果保留根号)
所经过的路径长是________.(结果保留根号)
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)①
;(3)①![]() ;②
;②![]()
【解析】
(1)观察图中![]() 和
和![]() 的数量关系可得
的数量关系可得![]() ,而
,而![]() ,将
,将![]() 代入即可.
代入即可.
(2)![]() 与
与![]() 的一边相切有两种情况,先与
的一边相切有两种情况,先与![]() 相切,再与
相切,再与![]() 相切;两种情况的解答方法都是连接圆心与切点,构造直角三角形,根据条件所给的特殊角的三角函数解答.
相切;两种情况的解答方法都是连接圆心与切点,构造直角三角形,根据条件所给的特殊角的三角函数解答.
(3)①根据旋转的性质可得![]() ,在
,在![]() 中根据三角函数可得
中根据三角函数可得![]() ,故当
,故当![]() 点与
点与![]() 点重合,
点重合,![]() 取得最大值时,
取得最大值时,![]() 有最大值,解之即可.
有最大值,解之即可.
②明显以![]() 点与
点与![]() 点重合前后为节点,点
点重合前后为节点,点![]() 的运动轨迹分两部分,第一部分为从
的运动轨迹分两部分,第一部分为从![]() 开始运动到
开始运动到![]() 点与
点与![]() 点重合,即图中的
点重合,即图中的![]() ,根据
,根据![]() 求解;第二部分,根据
求解;第二部分,根据![]() 为定值可知其轨迹为图中的
为定值可知其轨迹为图中的![]() ,在
,在![]() 中用勾股定理求解即可.
中用勾股定理求解即可.
(1)![]() ,
,![]()
(2)情况1:与![]() 相切时,
相切时,
![]() 中,∵
中,∵![]()
∴![]()
∴![]() 解得
解得![]()
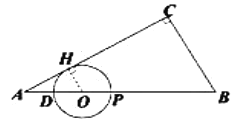
情况2:与![]() 相切时,
相切时,
![]() 中,∵
中,∵![]()
∴![]() 即
即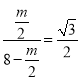
解得![]()
(3)①

在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴当![]() 最大时即
最大时即![]() 最大
最大
当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值最大.
的值最大.
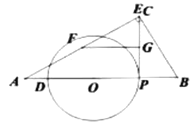
易知此时![]() .
.
在![]() 中,∵
中,∵![]() ∴
∴![]()
∴![]()
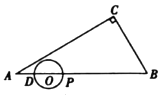
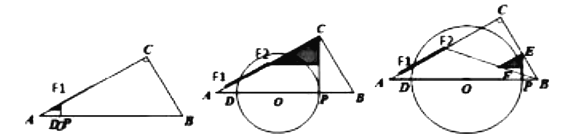
(3)![]() 轨迹如图:从
轨迹如图:从![]() 到
到![]() 到
到![]()
![]() ,
,
![]() ,
,
故![]() ,
,
![]() 到
到![]() 轨迹是线段理由如下:
轨迹是线段理由如下:
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() 为定值,
为定值,
∴点![]() 的第二段的轨迹是线段
的第二段的轨迹是线段![]() .
.
在![]() 中,
中,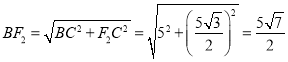 ,
,
所以点![]() 所经过的路径长是
所经过的路径长是![]() .
.

练习册系列答案
相关题目