题目内容
 某居民区一处圆形下水管道破裂,修理人员准备更换一段与原管道同样粗细的新管道.如图,水面宽度原有60cm,发现时水面宽度只有50
某居民区一处圆形下水管道破裂,修理人员准备更换一段与原管道同样粗细的新管道.如图,水面宽度原有60cm,发现时水面宽度只有50| 3 |
50
50
cm的管道.分析:过点O作HF⊥AE于点F,交CD于点H,根据CD∥AE可知EF⊥CD,连接OC,OA,设⊙O的半径为r,OH=h,则OF=25-h,在Rt△OCH与Rt△OAF中利用勾股定理即可求出r的值.
解答: 解:如图所示:过点O作HF⊥AH于点F,交CD于点H,连接OC,OA,
解:如图所示:过点O作HF⊥AH于点F,交CD于点H,连接OC,OA,
∵CD∥AE,
∴HF⊥CD,
∵CD=60cm,AE=50
cm,
∴CE=
CD=
×60=30cm,AF=
AE=
×50
=25
,
设⊙O的半径为r,OH=h,则OF=25-h,
在Rt△OCE中,OC2=CH2+OH2,即r2=302+h2,①
在Rt△OAF中,OA2=AF2+OF2,即r2=(25
)2+(25-h)2,②
①②联立,解得r=50cm.
故答案为:50.
 解:如图所示:过点O作HF⊥AH于点F,交CD于点H,连接OC,OA,
解:如图所示:过点O作HF⊥AH于点F,交CD于点H,连接OC,OA,∵CD∥AE,
∴HF⊥CD,
∵CD=60cm,AE=50
| 3 |
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
设⊙O的半径为r,OH=h,则OF=25-h,
在Rt△OCE中,OC2=CH2+OH2,即r2=302+h2,①
在Rt△OAF中,OA2=AF2+OF2,即r2=(25
| 3 |
①②联立,解得r=50cm.
故答案为:50.
点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
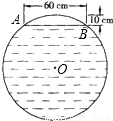
 银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60cm,水面至管道顶差距离为10cm,问修理人员应准备内径多大的管道?
银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60cm,水面至管道顶差距离为10cm,问修理人员应准备内径多大的管道? 某市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60cm,水面至管道顶差距离为10cm,修理人员应准备内径为( )cm的管道.
某市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60cm,水面至管道顶差距离为10cm,修理人员应准备内径为( )cm的管道.