题目内容
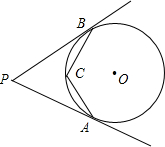
如图，PA、PB分别切⊙O于A、B，根据这些条件，你能得出哪些结论？（不再添字母和线段，半径相等除外，只写3个正确结论即可）
①________；②________；③________．（答案不唯一）
AP=BP OA2=OC•OP △AOP≌△BOP
分析：已知PA、PB分别切⊙O于A、B，则满足切线的性质定理，以及切线长定理，可以得到AC与OP互相垂直，根据条件进一步可以得到相似三角形，以及垂直关系．
解答：①AP=BP；②OA2=OC•OP；③△AOP≌△BOP．
点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
分析：已知PA、PB分别切⊙O于A、B，则满足切线的性质定理，以及切线长定理，可以得到AC与OP互相垂直，根据条件进一步可以得到相似三角形，以及垂直关系．
解答：①AP=BP；②OA2=OC•OP；③△AOP≌△BOP．
点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
如图，PA、PB分别切圆O于A、B两点，C为劣弧AB上一点，已知∠P=50°，则∠ACB=
7、如图，PA、PB分别切圆O于A、B两点，C为劣弧AB上一点，∠APB=30°，则∠ACB=（ ）
7、如图，PA，PB分别切⊙O于点A，B，点C是AB上一点，过C作⊙O的切线，交PA，PB于点D，E，若PA=6cm，则△PDE的周长是
（2012•绵阳）如图，PA、PB分别切⊙O于A、B，连接PO、AB相交于D，C是⊙O上一点，∠C=60°．
如图，PA，PB分别切⊙O于点A和点B，C是