Question

（2011•台州模拟）在□ABCD中，已知AB=5，BC=2

2

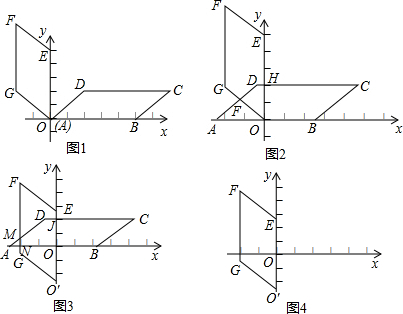
，∠A=45°，以AB所在直线为x轴，A为坐标原点建立直角坐标系，将□ABCD绕A点按逆时针方向旋转90°得到□OEFG（图1）
（1）直接写出C﹑F两点的坐标．
（2）沿x轴的负半轴以1米/秒的速度平行移动，设移动后x秒（图2），□ABCD与□OEFG重叠部分的面积为y，当点D移动到□OEFG的内部时，求y与x之间的关系式．
（3）若□ABCD与□OEFG同时从O点出发，分别沿x轴、y轴的负半轴以1米/秒的速度平行移动，设移动后x秒（如图3），□ABCD与□OEFG重叠部分的面积为y，当点D移动到□O'EFG的内部时，求y与x之间的关系式，并求出重叠部分面积的最大值．

Answer 1

分析：（1）根据勾股定理和坐标知识可求出C，F的坐标．
（2）因为∠DAB=∠GOA=45°，以及重叠部分的面积可用四边形AOHD和三角形AOF的面积来表示出来，从而可求出解析式．
（3）先求出表示面积的解析式，然后根据函数的最值求解．

解答：解：（1）C（7，2），F （-2，7）（4分）（2）设AD、DC分别与OG、OE交于点F、H
∵∠DAB=∠GOA=45°S_?OHDF=S_?AOHD-S_△AOF
∴OF=AF=

2

2

OA=

2

2

x，OH=2，DH=x-2
即y=

1

2

(DH+AO)•OH-

1

2

AF•?OFy=

1

2

(x+x-2)•×2-

1

2

×(

2 x

2

)2=-

1

4

x2+2x-2（2＜x＜4）（8分）
（3）①当2＜x≤3时，DE=x-2，OA=x，
∴y=

1

2

(x+x-2)×2-

1

2

(x-2)2
y=-

1

2

x2+4x-4=-

1

2

(x-4)2+4
当x=3时，y_max=4-

1

2

=

7

2

∴移动后3秒时，重叠部分面积的最大值是

7

2

（11分）
②当3＜x＜4时，延长CD与FG交于点Q，
QM=DQ=QN-MN，即QM=DQ=2-（x-2）=4-x
PJ=EJ=x+2-5=x-3，
∴y=2×2-

1

2

(4-x)2-

1

2

(x-3)2y=-x²+7x-

17

2

=-(x-

7

2

)2+

15

4

当x=

7

2

时，ymax=

15

4

∴移动后

7

2

秒时，重叠部分面积的最大值是

15

4

（13分）
综上①②所述，同时从O点移动

7

2

秒时，重叠部分面积的最大值是

15

4

（14分）

点评：本题考查了旋转的性质，平移的性质，二次函数的性质和最值的求法以及平行四边形的性质等知识点．