题目内容
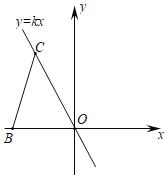
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() .直线
.直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.
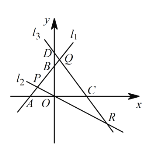
(1)点![]() 的坐标是 ,点
的坐标是 ,点![]() 的坐标是 ,点
的坐标是 ,点![]() 的坐标是 ;
的坐标是 ;
(2)将![]() 沿
沿![]() 轴折叠后,点
轴折叠后,点![]() 的对应点为
的对应点为![]() ,试判断点
,试判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(3)求![]() 的面积.
的面积.
【答案】(1)![]() ;
;![]() ;
;![]() ;(2)点
;(2)点![]() 在直线
在直线![]() 上,理由详见解析;(3)
上,理由详见解析;(3)![]()
【解析】
(1)直线l1:y=x+3与x轴交于点A,与y轴交于点B,令y=0,求得x=3,令x=0,求得y=3,得到A、B的坐标将直线l1:y=x+3和直线l2:y=![]() x联立组成有关x、y的方程组,解方程就能求出两直线的交点P坐标;
x联立组成有关x、y的方程组,解方程就能求出两直线的交点P坐标;
(2)求得P′的坐标,代入y=![]() x+4即可判断;
x+4即可判断;
(3)求得Q、R、C点的坐标,再过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,根据割补法即可求得.
,根据割补法即可求得.
(1)∵直线l1:y=x+3与x轴交于点A,与y轴交于点B,
∴令y=0,求得x=3,令x=0,求得y=3,
∴A(3,0)、B(0,3),
∵直线l1与直线l2:y=![]() x交于点P.
x交于点P.
∴解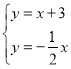 得
得
![]() ,
,
∴P(2,1),
故答案为:(3,0),(0,3),(2,1);
(2)点![]() 在直线
在直线![]() 上,理由如下:
上,理由如下:
因为![]() ,且将
,且将![]() 沿
沿![]() 轴折叠后,点
轴折叠后,点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
所以![]() ,
,
当![]() 时,代入
时,代入![]() 得
得![]() ,
,
所以点![]() 在直线
在直线![]() 上.
上.
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
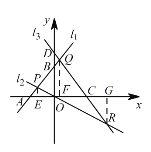
由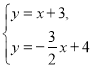 得
得
所以![]() ,
,
由 得
得![]()
所以![]() ,
,
对于![]() ,令
,令![]() 得
得![]() ,
,
所以![]() ,
,
∴![]() =
= ![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
所以![]() .
.

练习册系列答案
相关题目