Question

【题目】如图，已知AC⊥BC，垂足为C，AC=4，BC=3 ，将线段AC绕点A按逆时针方向旋转60°，得到线段AD，连接DC，DB．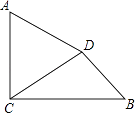
（1）线段DC=；
（2）求线段DB的长度．

Answer 1

【答案】
（1）4
（2）解：作DE⊥BC于点E．

∵△ACD是等边三角形，

∴∠ACD=60°，

又∵AC⊥BC，

∴∠DCE=∠ACB﹣∠ACD=90°﹣60°=30°，

∴Rt△CDE中，DE= DC=2，

CE=DCcos30°=4× =2 ，

∴BE=BC﹣CE=3 ﹣2 = ．

∴Rt△BDE中，BD= = = ．

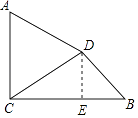
【解析】解：（1）∵AC=AD，∠CAD=60°， ∴△ACD是等边三角形，
∴DC=AC=4．
故答案是：4；
（1）证明△ACD是等边三角形，据此求解；（2）作DE⊥BC于点E，首先在Rt△CDE中利用三角函数求得DE和CE的长，然后在Rt△BDE中利用勾股定理求解．