题目内容
先阅读漫画,再解决漫画提出的问题.
题注:船顺水航行的速度=船静水航行的速度+水流速度;船逆水航行的速度=船静水航行的速度-水流速度;帽子漂流速度=水流速度.
渔夫在静水划船总是每小时5里,现在逆水行舟,水流速度是每小时3里;一阵风把他帽子吹落在水中,假如他没有发现,继续向前划行;等他发觉时人与帽子相距2.5里;
于是他立即原地调头追赶帽子,原地调转船头用了6分钟.

计算:
(1)从帽子丢失到发觉经过了多少时间?
(2)从发觉帽子丢失到捡回帽子经过了多少时间?
题注:船顺水航行的速度=船静水航行的速度+水流速度;船逆水航行的速度=船静水航行的速度-水流速度;帽子漂流速度=水流速度.
渔夫在静水划船总是每小时5里,现在逆水行舟,水流速度是每小时3里;一阵风把他帽子吹落在水中,假如他没有发现,继续向前划行;等他发觉时人与帽子相距2.5里;
于是他立即原地调头追赶帽子,原地调转船头用了6分钟.

计算:
(1)从帽子丢失到发觉经过了多少时间?
(2)从发觉帽子丢失到捡回帽子经过了多少时间?
分析:(1)根据逆水时船的速度以及水速表示出两者行驶的路程之和为2.5即可得出答案;
(2)根据小船顺水速度与帽子速度表示出两者行驶的路程,进而得出等式方程求出即可.
(2)根据小船顺水速度与帽子速度表示出两者行驶的路程,进而得出等式方程求出即可.
解答:解:(1)设从帽子丢失到发觉经过了x小时,
根据题意得出:
(5-3)x+3x=2.5,
解得:x=0.5,
答:从帽子丢失到发觉经过了0.5小时;
(2)设从发觉帽子丢失到捡回帽子经过了y小时,
根据题意得出:(5+3)(y-
)-2.5=3y,
整理得出:5y=3.3,
解得:y=0.66,
答:从发觉帽子丢失到捡回帽子经过了0.66小时.
根据题意得出:
(5-3)x+3x=2.5,
解得:x=0.5,
答:从帽子丢失到发觉经过了0.5小时;
(2)设从发觉帽子丢失到捡回帽子经过了y小时,
根据题意得出:(5+3)(y-
| 6 |
| 60 |
整理得出:5y=3.3,
解得:y=0.66,
答:从发觉帽子丢失到捡回帽子经过了0.66小时.
点评:此题主要考查了一元一次方程的应用,根据已知表示出小船与了、帽子行驶路程是解题关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 先阅读短文,再回答短文后面的问题.
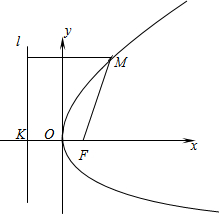
先阅读短文,再回答短文后面的问题.平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l叫做抛物线的准线.
下面根据抛物线的定义,我们来求抛物线的方程.
如上图,建立直角坐标系xoy,使x轴经过点F且垂直于直线l,垂足为K,并使原点与线段KF的中点重合.设|KF|=p(p>0),那么焦点F的坐标为(
| p |
| 2 |
| p |
| 2 |
设点M(x,y)是抛物线上任意一点,点M到l的距离为d,由抛物线的定义,抛物线就是满足|MF|=d的点M的轨迹.
∵|MF|=
(x-
|
| p |
| 2 |
(x-
|
| p |
| 2 |
将上式两边平方并化简,得y2=2px(p>0)①
方程①叫做抛物线的标准方程,它表示的抛物线的焦点在x轴的正半轴上,坐标是(
| p |
| 2 |
| p |
| 2 |
一条抛物线,由于它在坐标平面内的位置不同,方程也不同.所以抛物线的标准方程还有其它的几种形式:y2=-2px,x2=2py,x2=-2py.这四种抛物线的标准方程,焦点坐标以及准线方程列表如下:
| 标准方程 | 交点坐标 | 准线方程 | ||||
| y2=2px(p>0) | (
|
x=-
| ||||
| y2=-2px(p>0) | (-
|
x=
| ||||
| x2=2py(p>0) | (0,
|
y=-
| ||||
| x2=-2py(p>0) | (0,-
|
y=-
|
(1)①已知抛物线的标准方程是y2=8x,则它的焦点坐标是
②已知抛物线的焦点坐标是F(0,-6),则它的标准方程是
(2)点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.
(3)直线y=
| 3 |
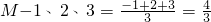 ,min{-1、2、3}=-1;
,min{-1、2、3}=-1;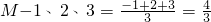 ,
,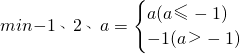 .
.