题目内容
【备用题】△ABC中，∠C=90，AC=4，BC=3． AB=5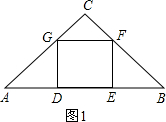
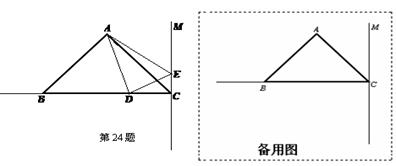
（1）如图（1），四边形DEFG为△ABC的内接正方形，求正方形的边长；
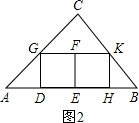
（2）如图（2），三角形内有并排的两个相等的正方形，它们组成的矩形内接于△ABC，求正方形的边长；
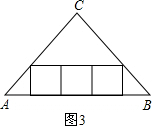
（3）如图（3），三角形内有并排的三个相等的正方形，它们组成的矩形内接于△ABC，求正方形的边长；
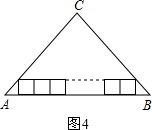
（4）如图（4），三角形内有并排的N个相等的正方形，它们组成的矩形内接于△ABC，求正方形的边长．
分析：本题中有很多对三角形相似，但与已知条件及所求的正方形边长相联系并没有，
因此，在图中作△ABC的高CN，交GF于M，利用相似三角形对应高的比等于相似比求解．
因此，在图中作△ABC的高CN，交GF于M，利用相似三角形对应高的比等于相似比求解．
解答：
解：（1）如图，在△ABC中，由AC=4，BC=3．AB=5，
AC•BC=
AB•CN得CN=
，
由GF∥AB得△CGF∽△CAB，
∴
=
；
设正方形的边长为x，则
=
，
解得x=
，
同理可得：（2）
（3）
（4）
．
解：（1）如图，在△ABC中，由AC=4，BC=3．AB=5，| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
由GF∥AB得△CGF∽△CAB，
∴
| CM |
| CN |
| GF |
| AB |
设正方形的边长为x，则
| ||
|
| x |
| 5 |
解得x=
| 60 |
| 37 |
同理可得：（2）
| 60 |
| 49 |
| 60 |
| 61 |
| 60 |
| 25+12n |
点评：熟练掌握相似三角形的判定及性质．
练习册系列答案
阅读快车系列答案
相关题目
？
？