题目内容
2. 如图是抛物线y=ax2+bx+c(a≠0)的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a+b<0;③$\frac{c}{a}$=-5;④如果点(3,y1)和点(6,y2)都在抛物线上,那么y1>y2;⑤方程ax2+bx+c=0的两个根是-1,5.其中正确的结论是( )
如图是抛物线y=ax2+bx+c(a≠0)的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a+b<0;③$\frac{c}{a}$=-5;④如果点(3,y1)和点(6,y2)都在抛物线上,那么y1>y2;⑤方程ax2+bx+c=0的两个根是-1,5.其中正确的结论是( )| A. | ①②⑤ | B. | ②④ | C. | ①③⑤ | D. | ③④ |
分析 根据开口向上,a>0,交y轴的负半轴,c<0,对称轴在y轴右侧,b<0,判断①;根据对称轴为x=2,判断②;根据对称轴和增减性判断③④⑤.
解答 解:①开口向上,a>0,交y轴的负半轴,c<0,对称轴在y轴右侧,b<0,∴abc>0,①正确;
②-$\frac{b}{2a}$=2,4a+b=0,②不正确;,④不正确.
③对称轴为x=2,与x轴的一个交点是(-1,0),则与x轴的另一个交点是(5,0),
所以方程ax2+bx+c=0的两个根是-1,5,$\frac{c}{a}$=-5,所以③⑤正确;
④如图,在对称轴的右侧,y随x的增大而增大,∴y1<y2,④不正确.
故选:C.
点评 本题考查的是二次函数图象与系数的关系,解题的关键是掌握二次函数的性质:开口方向、对称轴、增减性,解答时,要灵活运用性质和图象.

练习册系列答案
相关题目
10.下列方程中,解为2的是( )
| A. | 3x+6=0 | B. | $-\frac{1}{4}x+\frac{1}{2}=0$ | C. | $-\frac{x}{2}=1$ | D. | 3-2x=1 |
14.下列说法正确的是( )
| A. | 正整数、负整数、分数统称为有理数 | B. | 整数包括正整数、0、负整数 | ||
| C. | 近似数3.10精确到了十分位 | D. | -24底数是-2,指数是4 |
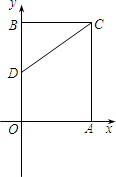 在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴y轴的正半轴上,OA=3,OB=4,D为OB的中点,点E为边OA上的一个动点.
在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴y轴的正半轴上,OA=3,OB=4,D为OB的中点,点E为边OA上的一个动点. 如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b 的图象经过点B(0,-1),并且与x轴以及y=x+1的图象分别交于点C、D.
如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b 的图象经过点B(0,-1),并且与x轴以及y=x+1的图象分别交于点C、D.