题目内容
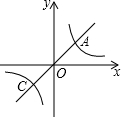 如图,直线y=x与双曲线y=
如图,直线y=x与双曲线y= 交于点A、C,且OA=OC=
交于点A、C,且OA=OC=
(1)求点A的坐标;
(2)以AC为对角线作矩形ABCD交x轴正半轴于B,交x轴负半轴于D,求点B、D坐标.
解: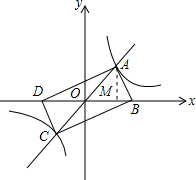 (1)∵点A在直线y=x上,设A(a,a),a>0.
(1)∵点A在直线y=x上,设A(a,a),a>0.
作AM⊥x轴于M,
∴OM=AM=a,
在Rt△AOM中,由勾股定理,
得OM2+AM2=OA2,
∴a2+a2= ,且a>0,
,且a>0,
∴a=1,
∴A(1,1);
(2)∵四边形ABCD是矩形,
∴AO=BO=CO=DO,
∴BO=OD= ,
,
∵点B在x轴的正半轴,点D在x轴的负半轴,
∴B( ,0),D(-
,0),D(- ,0).
,0).
分析:(1)根据点A在直线y=x上可设A(a,a),a>0.作AM⊥x轴于M,故可得出OM=AM=a,在Rt△AOM中根据勾股定理即可得出a的值,故可得出A点坐标;
(2)根据四边形ABCD是矩形可知AO=BO=CO=DO= ,再由点B在x轴的正半轴,点D在x轴的负半轴上即可得出结论.
,再由点B在x轴的正半轴,点D在x轴的负半轴上即可得出结论.
点评:本题考查的是反比例函数综合题,涉及到勾股定理及矩形的性质,比较简单.
 (1)∵点A在直线y=x上,设A(a,a),a>0.
(1)∵点A在直线y=x上,设A(a,a),a>0.作AM⊥x轴于M,
∴OM=AM=a,
在Rt△AOM中,由勾股定理,
得OM2+AM2=OA2,
∴a2+a2=
 ,且a>0,
,且a>0,∴a=1,
∴A(1,1);
(2)∵四边形ABCD是矩形,
∴AO=BO=CO=DO,
∴BO=OD=
 ,
,∵点B在x轴的正半轴,点D在x轴的负半轴,
∴B(
 ,0),D(-
,0),D(- ,0).
,0).分析:(1)根据点A在直线y=x上可设A(a,a),a>0.作AM⊥x轴于M,故可得出OM=AM=a,在Rt△AOM中根据勾股定理即可得出a的值,故可得出A点坐标;
(2)根据四边形ABCD是矩形可知AO=BO=CO=DO=
 ,再由点B在x轴的正半轴,点D在x轴的负半轴上即可得出结论.
,再由点B在x轴的正半轴,点D在x轴的负半轴上即可得出结论.点评:本题考查的是反比例函数综合题,涉及到勾股定理及矩形的性质,比较简单.

练习册系列答案
相关题目
 如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=
如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=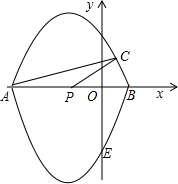 点,且P(-1,0),C(
点,且P(-1,0),C(


