题目内容
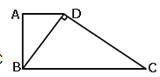
【题目】如图,ΔABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=APAB;④ABCP=APCB,任选一个,使ΔAPC与ΔACB相似的条件可以是( )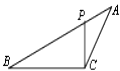
A.①或②或③
B.①或③或④
C.②或③或④
D.①或②或④
【答案】A
【解析】①∵∠ACP=∠B,∠A=∠A,
∴△APC∽△ACB;
②∵∠APC=∠ACB,∠A=∠A,
∴△APC∽△ACB;
③∵AC2=APAB;∠A=∠A,
∴△APC∽△ACB;
④∵ABCP=APCB
不能得到△APC与△ACB相似;
所以答案是:A.
【考点精析】掌握相似三角形的判定是解答本题的根本,需要知道相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目