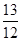题目内容
如果实数a,b,c满足a2+b2+c2=ab+bc+ca,那么
- A.a,b,c全相等
- B.a,b,c不全相等
- C.a,b,c全不相等
- D.a,b,c可能相等,也可能不等
A
分析:由题意实数a,b,c满足a2+b2+c2=ab+bc+ca,把其凑成完全平方式然后求解.
解答:∵a2+b2+c2=ab+ac+bc,
∴2a2+2b2+2c2=2(ab+ac+bc),
∴a2+b2-2ab+a2+c2-2ac+b2+c2-2bc=0,
∴(a-b)2+(a-c)2+(b-c)2=0,
又∵(a-b)2≥0,(a-c)2≥0,(b-c)2≥0,
∴a=b且a=c,即a=b=c,
故选A.
点评:此题主要考查完全平方式的性质,解题的关键是把已知条件凑成完全平方式.
分析:由题意实数a,b,c满足a2+b2+c2=ab+bc+ca,把其凑成完全平方式然后求解.
解答:∵a2+b2+c2=ab+ac+bc,
∴2a2+2b2+2c2=2(ab+ac+bc),
∴a2+b2-2ab+a2+c2-2ac+b2+c2-2bc=0,
∴(a-b)2+(a-c)2+(b-c)2=0,
又∵(a-b)2≥0,(a-c)2≥0,(b-c)2≥0,
∴a=b且a=c,即a=b=c,
故选A.
点评:此题主要考查完全平方式的性质,解题的关键是把已知条件凑成完全平方式.

练习册系列答案
相关题目
 有两个不相等的实数根x1,x2,求k的取值范围.
有两个不相等的实数根x1,x2,求k的取值范围.

 >0
>0
 有两个不相等的实数根x1,x2,求k的取值范围.
有两个不相等的实数根x1,x2,求k的取值范围.

 >0
>0
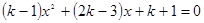 有两个不相等的实数根x1,x2,求k的取值范围.
有两个不相等的实数根x1,x2,求k的取值范围.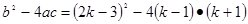
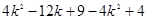
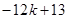 >0
>0