题目内容
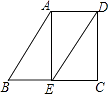
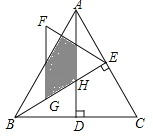
【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=![]() ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
【答案】![]() .
.
【解析】
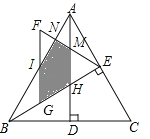
试题分析:如图所示,由△ABC是等边三角形,BC=![]() ,得到AD=BE=
,得到AD=BE=![]() BC=6,∠ABG=∠HBD=30°,由直角三角的性质,得∠BHD=90°﹣∠HBD=60°,由对顶角相等,得∠MHE=∠BHD=60°,由BG=2,得EG=BE﹣BG=6﹣2=4.由GE为边作等边三角形GEF,得FG=EG=4,∠EGF=∠GEF=60°,△MHE是等边三角形;S△ABC=
BC=6,∠ABG=∠HBD=30°,由直角三角的性质,得∠BHD=90°﹣∠HBD=60°,由对顶角相等,得∠MHE=∠BHD=60°,由BG=2,得EG=BE﹣BG=6﹣2=4.由GE为边作等边三角形GEF,得FG=EG=4,∠EGF=∠GEF=60°,△MHE是等边三角形;S△ABC=![]() ACBE=
ACBE=![]() AC×EH×3EH=
AC×EH×3EH=![]() BE=
BE=![]() ×6=2.由三角形外角的性质,得∠BIF=∠FGE﹣∠IBG=60°﹣30°=30°,由∠IBG=∠BIG=30°,得IG=BG=2,由线段的和差,得IF=FG﹣IG=4﹣2=2,由对顶角相等,得∠FIN=∠BIG=30°,由∠FIN+∠F=90°,得∠FNI=90°,由锐角三角函数,得FN=1,IN=
×6=2.由三角形外角的性质,得∠BIF=∠FGE﹣∠IBG=60°﹣30°=30°,由∠IBG=∠BIG=30°,得IG=BG=2,由线段的和差,得IF=FG﹣IG=4﹣2=2,由对顶角相等,得∠FIN=∠BIG=30°,由∠FIN+∠F=90°,得∠FNI=90°,由锐角三角函数,得FN=1,IN=![]() .S五边形NIGHM=S△EFG﹣S△EMH﹣S△FIN=
.S五边形NIGHM=S△EFG﹣S△EMH﹣S△FIN=![]() =
=![]() ,故答案为:
,故答案为:![]() .
.

练习册系列答案
相关题目