Question

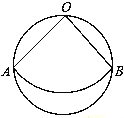
【题目】如图，从直径为2cm的圆形纸片中，剪出一个圆心角为90°的扇形OAB，且点O、A、B在圆周上，把它围成一个圆锥，则圆锥的底面圆的半径是 cm．

Answer 1

【答案】．

【解析】

试题分析：本题考查了圆锥的计算：圆锥的侧面展开图为扇形，扇形的弧长等于圆锥底面圆的周长，扇形的半径等于圆锥的母线长．也考查了圆周角定理和弧长公式．设圆锥的底面圆的半径为r，由∠AOB=90°得到AB为圆形纸片的直径，则OB=AB=cm，根据弧长公式计算出扇形OAB的弧AB的长，然后根据圆锥的侧面展开图为扇形，扇形的弧长等于圆锥底面圆的周长进行计算．

解：设圆锥的底面圆的半径为r，

连结AB，如图，

∵扇形OAB的圆心角为90°，

∴∠AOB=90°，

∴AB为圆形纸片的直径，

∴AB=2cm，

∴OB=AB=cm，

∴扇形OAB的弧AB的长==π，

∴2πr=π，

∴r=（cm）．

故答案为：．