题目内容
(1)先化简,再求值: ,其中a=
,其中a= +1(精确到0.01);
+1(精确到0.01);
(2)当b≠0时,比较 与1的大小.
与1的大小.
解:(1)原式= •
• -
- •
• =3(a-1)-
=3(a-1)-
当a= +1时,
+1时,
原式=3( +1)-
+1)-
=3 +3-
+3-
=3 +3-
+3-
=3 +3-
+3-
=3 +3-
+3- -
-
= -
-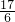
=
≈
=2.02;
(2)因为b+1<0时二次根式无意义,所以:
①0<b+1<1时, <1;
<1;
②b+1=1时, =1;
=1;
③b+1>1时, >1.
>1.
分析:(1)利用平方差公式将(a2-1)展开,以便于化简,然后再求值;
(2)因为b+1<0时无意义,所以应分0<b+1<1,b+1=1,b+1>1三种情况讨论.
点评:(1)先化简,再求值可以减小计算量,解答时要注意分母有理化及乘法公式的运用;
(2)要根据二次根式成立的条件及二次根式的意义分类讨论.
 •
• -
- •
• =3(a-1)-
=3(a-1)-
当a=
 +1时,
+1时,原式=3(
 +1)-
+1)-
=3
 +3-
+3-
=3
 +3-
+3-
=3
 +3-
+3-
=3
 +3-
+3- -
-
=
 -
-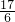
=

≈

=2.02;
(2)因为b+1<0时二次根式无意义,所以:
①0<b+1<1时,
 <1;
<1;②b+1=1时,
 =1;
=1;③b+1>1时,
 >1.
>1.分析:(1)利用平方差公式将(a2-1)展开,以便于化简,然后再求值;
(2)因为b+1<0时无意义,所以应分0<b+1<1,b+1=1,b+1>1三种情况讨论.
点评:(1)先化简,再求值可以减小计算量,解答时要注意分母有理化及乘法公式的运用;
(2)要根据二次根式成立的条件及二次根式的意义分类讨论.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目