题目内容
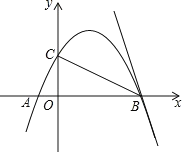
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() 为
为![]() 的中点.
的中点.
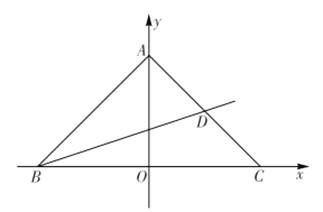
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 以每秒
以每秒![]() 个单位长度的速度运动,运动时间为
个单位长度的速度运动,运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() 求
求![]() 与
与![]() 的函数关系式,并直接写出自变量的取值范围;
的函数关系式,并直接写出自变量的取值范围;
(3)在(2)的条件下,是否存在点![]() 使
使![]() 是以
是以![]() 为腰的等腰三角形,若存在,直接写出点
为腰的等腰三角形,若存在,直接写出点![]() 的坐标;若不存在;请说明理由.
的坐标;若不存在;请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在
;(3)存在![]() ,
,![]() .
.
【解析】
(1)根据已知条件可得出点A、B的坐标,再根据![]() 得出点C的坐标,再利用待定系数法求直线AC解析式即可;
得出点C的坐标,再利用待定系数法求直线AC解析式即可;
(2)先求出点D的坐标为![]() ,利用勾股定理可得出
,利用勾股定理可得出![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,利用三角形的面积可得出AF的值,当运动时间为
,利用三角形的面积可得出AF的值,当运动时间为![]() 秒时,
秒时,![]() ,分点
,分点![]() 在线段
在线段![]() 上运动时,即
上运动时,即![]() 时和点
时和点![]() 在线段
在线段![]() 延长线上运动时,即
延长线上运动时,即![]() 时两种情况分析.
时两种情况分析.
(3)分![]() 和
和![]() 两种情况,当
两种情况,当![]() 时,
时,![]() ,但
,但![]() 不垂直
不垂直![]() ,此种情况不符合题意;当
,此种情况不符合题意;当![]() 时,可知点
时,可知点![]() 的纵坐标为
的纵坐标为![]() ,可得
,可得![]() ,解方程即可.
,解方程即可.
解:![]() 令
令![]() 中
中![]()
则![]() .
.
![]()
令![]() 中
中![]()
则![]()
![]()
![]() 点
点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]()
设直线![]() 的解析式为
的解析式为![]()
将点![]() 代入
代入![]() 中,
中,
得![]()
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
![]() 为
为![]() 的中点,
的中点,
![]() 点
点![]() 的坐标为
的坐标为![]()
![]() .
.
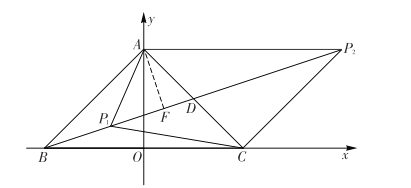
过点![]() 作
作![]() 交
交![]() 于点
于点![]() 如图,
如图,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
当点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 以每秒
以每秒![]() 个单位长度的速度运动,
个单位长度的速度运动,
运动时间为![]() 秒时,
秒时,![]()
当点![]() 在线段
在线段![]() 上运动时,即
上运动时,即![]() 时,
时,
![]()
![]()
![]() ;
;
当点![]() 在线段
在线段![]() 延长线上运动时,即
延长线上运动时,即![]() 时,
时,
![]()
![]()
![]()
综上所述:![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
![]() 存在
存在![]() ,
,![]() .
.
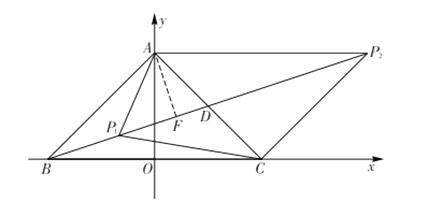
如图,要使![]() 是等腰三角形,且以
是等腰三角形,且以![]() 为腰,有两种情况:
为腰,有两种情况:
![]()
![]() 但
但![]() 不垂直
不垂直![]()
![]() 此种情况不存在;
此种情况不存在;
![]() ,由题意,可知点
,由题意,可知点![]() 的纵坐标为
的纵坐标为![]()
可得![]()
解得![]()
![]() ,
,![]()

【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?