题目内容
【题目】已知抛物线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,交y轴于点
,交y轴于点![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线解析式;
(2)在第一象限内的抛物线上求点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
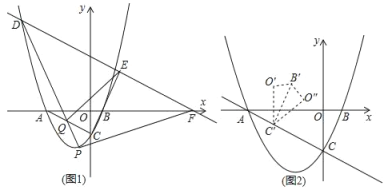
(3)![]() 是第一象限内抛物线上一点,
是第一象限内抛物线上一点,![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 在
在![]() 点右侧,且满足
点右侧,且满足![]() ,当
,当![]() 为何值时,满足条件的点
为何值时,满足条件的点![]() 只有一个?
只有一个?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
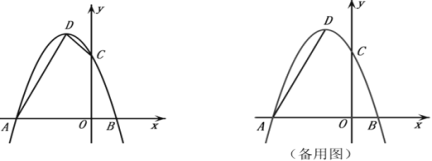
(1)已知抛物线过定点,用待定系数法即可求解;(2)过点D作DH⊥y轴交y轴于点H,DH=HC,OA=OC,∠DHC=∠AOC=90°得△DHC和△AOC都是等腰直角三角形,从而得出∠DCH=∠ACO=45°,DC=![]() ,AC=
,AC=![]() ,∠ACD=90°,DC⊥AC,延长DC至N使CN=DC=
,∠ACD=90°,DC⊥AC,延长DC至N使CN=DC=![]() ,根据
,根据![]() ,
,![]() ,得出S△ADC=S△ACM,得出直线AC的解析式为:y=x+3,从而得出直线NM的解析式为:y=x+1,由
,得出S△ADC=S△ACM,得出直线AC的解析式为:y=x+3,从而得出直线NM的解析式为:y=x+1,由![]() 求得点M的坐标为:
求得点M的坐标为:![]() ;(3)延长DF交x轴于点E,过点D作DG⊥x轴交x轴于点G,设OE=a,则EA=ED=a+3,GE=a+1,在Rt△DGE中,DG2+GE2=DE2,解得a=2,解得E(2,0)得直线DE的解析式为:
;(3)延长DF交x轴于点E,过点D作DG⊥x轴交x轴于点G,设OE=a,则EA=ED=a+3,GE=a+1,在Rt△DGE中,DG2+GE2=DE2,解得a=2,解得E(2,0)得直线DE的解析式为:![]() ,联立
,联立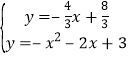 ,由此可得
,由此可得![]() ,由∠APF是△DPF的一个外角,可得△FDP≌△PAQ,
,由∠APF是△DPF的一个外角,可得△FDP≌△PAQ,![]() ,易得
,易得![]() ,
,![]() ,,设DP=x,则PA=
,,设DP=x,则PA=![]() ,则AQ=m+3,由
,则AQ=m+3,由![]() ,整理得
,整理得![]() ,令△=0,解得
,令△=0,解得![]() .
.
(1)依题有![]()
解得,![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
由(1)得,![]()
![]() ,
,![]() ,
,
又![]() ,
,
![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
延长![]() 至
至![]() 使
使![]() ,
,
易得![]()
过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
依题有![]() 的解析式为:
的解析式为:![]() ,
,
设![]() 的解析式为:
的解析式为:![]()
将点![]() 代入
代入![]() 的解析式得,
的解析式得,![]() ,
,
![]() 的解析式为:
的解析式为:![]() ,
,
联立![]()
解得,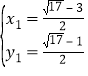 ,
, 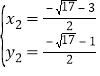 (舍去)
(舍去)
![]() ;
;
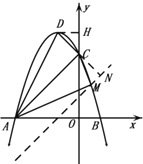
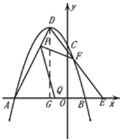
(3)如图,延长![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]()
![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]()
即![]() ,解得,
,解得,![]() .
.
![]()
![]() 直线的解析式为:
直线的解析式为:![]()
联立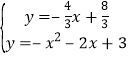
解得: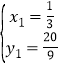 ,
,![]() ,
,
![]() 是第一象限内抛物线上一点,
是第一象限内抛物线上一点,
![]()
![]() 是
是![]() 的一个外角,
的一个外角,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
易得,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
依题有![]() ,
,
![]() ,
,
![]() ,
,
整理得,![]() ,
,
![]() .
.
∵当![]() 时,满足条件的
时,满足条件的![]() 只有一个,
只有一个,
![]() ,
,
解得,![]() .
.

 阅读快车系列答案
阅读快车系列答案