题目内容
18.某中学准备购买一些排球,现商店有A、B两种品牌的排球,已知购买1个A品牌排球和购买2个B品牌排球一共花200元,购买2个A品牌排球比购买3个B品牌排球少花20元.(1)分别求A品牌排球和B品牌排球的单价;(要求列方程(组)进行解答)
(2)学校准备用不超过650元来购买A、B两种品牌的排球共10个(两种排球都要买),问有几种购买方案?(要求列不等式进行解答)
分析 (1)设A品牌排球的单价为x元、B品牌排球的单价为y元,根据关键语句“购买1个A品牌排球和购买2个B品牌排球一共花200元,购买2个A品牌排球比购买3个B品牌排球少花20元”可得方程组,解方程组可得答案;
(2)设设购买A品牌排球m个,则购买B品牌排球(10-m)个,根据关键语句“不超过650元来购买A、B两种品牌的排球共10个”可得不等式,再解不等式即可.
解答 解:(1)设A品牌排球的单价为x元、B品牌排球的单价为y元,
根据题意,得$\left\{\begin{array}{l}x+2y=200\\ 3y-2x=20\end{array}\right.$,
解这个方程组,得 $\left\{\begin{array}{l}x=80\\ y=60\end{array}\right.$.
答:A、B品牌排球的单价分别为80元、60元;
(2)设购买A品牌排球m个,则购买B品牌排球(10-m)个,
根据题意,得 80m+60(10-m)≤650,
解得 m≤2.5,
由题意,知 m必须为正整数,
∴m=1或m=2,
∴一共有两种购买方案:
方案一:当m=1,10-m=9时,即购买A品牌排球1个,B品牌排球9个;
方案二:当m=2,10-m=8时,购买A品牌排球2个,B品牌排球8个.
点评 此题主要考查了一元一次不等式和二元一次方程组的应用,关键是弄清题意,根据关键语句算出A品牌排球和B品牌排球的单价.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
8.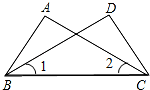 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是( )
 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是( )| A. | AB=CD | B. | AC=BD | C. | ∠A=∠D | D. | ∠ABC=∠DCB |

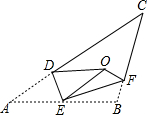 如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为=41°.
如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为=41°.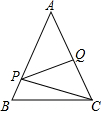 图中,P及Q分别为AB及AC上的点使得PQ为△APC的一条垂直平分线,若QC=6cm及△BCP的周长为21cm,求△ABC的周长.
图中,P及Q分别为AB及AC上的点使得PQ为△APC的一条垂直平分线,若QC=6cm及△BCP的周长为21cm,求△ABC的周长.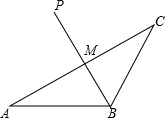 图中,△ABC为一钝角三角形,P为△ABC的外心,PB与AC相交于M.
图中,△ABC为一钝角三角形,P为△ABC的外心,PB与AC相交于M.