题目内容
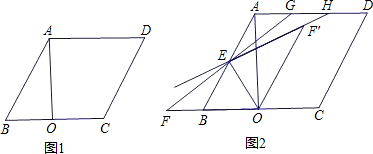
如图1,在?ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.如图2,E,F是平行四边形ABCD的对角线AC上的点,CE=AF. 请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.

(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.如图2,E,F是平行四边形ABCD的对角线AC上的点,CE=AF. 请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.

分析:(1)由在?ABCD中,E、F分别是AB、CD的中点,利用SAS即可判定:△BEC≌△DFA;
(2)易证得四边形AECF是平行四边形,又由CA=CB,E是AB的中点,解得CE⊥AB,继而证得四边形AECF是矩形;
易证得△ADF≌△CBE,则可证得BE=DF,BE∥DF.
(2)易证得四边形AECF是平行四边形,又由CA=CB,E是AB的中点,解得CE⊥AB,继而证得四边形AECF是矩形;
易证得△ADF≌△CBE,则可证得BE=DF,BE∥DF.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
∵E、F分别是AB、CD的中点,
∴BE=
AB,DF=
CD,
在△BEC和△DFA中,
,
∴△BEC≌△DFA(SAS);
(2)四边形AECF是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=DF,
∵AE=CF,
∴四边形AECF是平行四边形,
∵CA=CB,E是AB的中点,
∴CE⊥AB,
∴∠AEC=90°,
∴平行四边形AECF是矩形.
猜想:BE=DF,且BE∥DF;
证明:∵四边形ABCD是平行四边形,
∴BC=AD,AD∥BC,
∴∠DAF=∠BCE,
在△ADF和△CBE中,
,
∴△BCE≌△DAF(SAS).
∴BE=DF,∠AFD=∠CEB.
∴BE∥DF.
∴BE=DF,且BE∥DF.
∴AB=CD,AD=BC,∠B=∠D,
∵E、F分别是AB、CD的中点,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
在△BEC和△DFA中,
|
∴△BEC≌△DFA(SAS);
(2)四边形AECF是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=DF,
∵AE=CF,
∴四边形AECF是平行四边形,
∵CA=CB,E是AB的中点,

∴CE⊥AB,
∴∠AEC=90°,
∴平行四边形AECF是矩形.
猜想:BE=DF,且BE∥DF;
证明:∵四边形ABCD是平行四边形,
∴BC=AD,AD∥BC,
∴∠DAF=∠BCE,
在△ADF和△CBE中,
|
∴△BCE≌△DAF(SAS).
∴BE=DF,∠AFD=∠CEB.
∴BE∥DF.
∴BE=DF,且BE∥DF.
点评:此题考查了平行四边形的性质、全等三角形的判定与性质以及矩形的判定.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
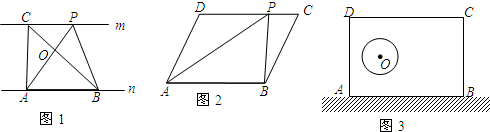



 )时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
)时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.