Question

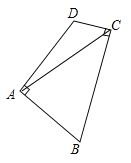
【题目】如图，AB∥CD，E为AB上一点，∠BED=2∠BAD．

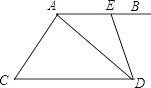
（1）求证：AD平分∠CDE；

（2）若AC⊥AD，∠ACD+∠AED=165°，求∠ACD的度数．

Answer 1

【答案】（1）见解析；（2）55°

【解析】

（1）根据平行线的性质得到∠BED=∠EDC，∠BAD=∠ADC，利用等量代换得到∠EDC=2∠ADC，由角平分线的定义即可得到结论；
（2）利用列方程的方式，设∠ADC=∠ADE=∠BAD=x，于是得到∠BED=∠EDC=2x，∠AED=180°-2x，根据平行线的性质得到∠BAC+∠ACD=180°，于是列方程90°-x+180°-2X=165°，即可得到结论．

（1）证明：∵AB∥CD，

∴∠BED=∠EDC，∠BAD=∠ADC，

∵∠BED=∠BAD+∠ADE，

∵∠BED=2∠BAD，

∴∠BAD=∠ADE，∠ADE=∠ACD，

∴AD平分∠CDE；

（2）解：依题意设∠ADC=∠ADE=∠BAD=x，

∴∠BED=∠EDC=2x，∠AED=180°﹣2x，

∵AB∥CD，

∴∠BAC+∠ACD=180°，即∠ACD=90°﹣x，

又∵∠ACD+∠AED=165°，

即90°﹣x+180°﹣2x=165°，

∴x=35°，

∴∠ACD=90°﹣x=90°﹣35°=55°．