题目内容
如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h1、h2、h3,△ABC的高为h.
在图1中,点P是边BC的中点,此时h3=0,可得结论:h1+h2+h3=h.
在图2,图3,图4,图5中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)请探究:图2,图3,图4,图5中,h1、h2、h3、h之间的关系;(直接写出结论)
(2)证明图2所得结论;
(3)证明图4所得结论;
(4)(附加题)在图6中,若四边形RBCS是等腰梯形,∠B=∠C=60°,RS=n,BC=m,点P在梯形内,且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4,桥形的高为h,则h1、h2、h3、h4、h之间的关系为:h1+h3+h4= .图4与图6中的等式有何关系.
.图4与图6中的等式有何关系.
在图1中,点P是边BC的中点,此时h3=0,可得结论:h1+h2+h3=h.
在图2,图3,图4,图5中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)请探究:图2,图3,图4,图5中,h1、h2、h3、h之间的关系;(直接写出结论)
(2)证明图2所得结论;
(3)证明图4所得结论;
(4)(附加题)在图6中,若四边形RBCS是等腰梯形,∠B=∠C=60°,RS=n,BC=m,点P在梯形内,且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4,桥形的高为h,则h1、h2、h3、h4、h之间的关系为:h1+h3+h4=
 .图4与图6中的等式有何关系.
.图4与图6中的等式有何关系.
解:(1)图2﹣5中的关系依次是:
h1+h2+h3=h;h1﹣h2+h3=h;h1+h2+h3=h;h1+h2﹣h3=h;
(2)图2中,h1+h2+h3=h.
∵h1=BPsin60°,h2=PCsin60°,h3=0,
∴h1+h2+h3=BPsin60°+PCsin60°=BCsin60°=ACsin60°=h;
(3)证明:图4中,h1+h2+h3=h.
过点P作RS∥BC与边AB、AC相交于R、S.
在△ARS中,由图2中结论知:h1+h2+0=h﹣h3.
∴h1+h2+h3=h.
(4)由(3)可知:h1+h3+h4= .
.
将R、S延BR、CS延长线向上平移,
当n=0时,图6变为图4,上面的等式就是图4中的等式,
所以上面结论是图4中结论的推广.
h1+h2+h3=h;h1﹣h2+h3=h;h1+h2+h3=h;h1+h2﹣h3=h;
(2)图2中,h1+h2+h3=h.
∵h1=BPsin60°,h2=PCsin60°,h3=0,
∴h1+h2+h3=BPsin60°+PCsin60°=BCsin60°=ACsin60°=h;
(3)证明:图4中,h1+h2+h3=h.
过点P作RS∥BC与边AB、AC相交于R、S.
在△ARS中,由图2中结论知:h1+h2+0=h﹣h3.
∴h1+h2+h3=h.
(4)由(3)可知:h1+h3+h4=
 .
.将R、S延BR、CS延长线向上平移,
当n=0时,图6变为图4,上面的等式就是图4中的等式,
所以上面结论是图4中结论的推广.


练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
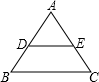
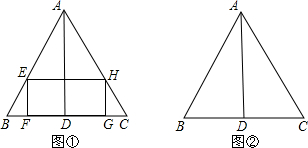
 (2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
(2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动