题目内容
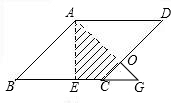 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折至△AGE,那么△AGE与四边形AECD重叠部分的面积是________.
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折至△AGE,那么△AGE与四边形AECD重叠部分的面积是________.
2 -2
-2
分析:阴影部分面积=S△ABG-S△COG-S△ABE.
解答:在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,故AE= ,
,
由折叠易得△ABG为等腰直角三角形,
∴S△ABG= BA•AG=2,S△ABE=1,
BA•AG=2,S△ABE=1,
∴CG=2BE-BC=2 -2,
-2,
∵AB∥CD,∴∠OCG=∠B=45°,
又由折叠的性质知,∠G=∠B=45°,
∴CO=OG=2- .∴S△COG=3-2
.∴S△COG=3-2 ,
,
∴重叠部分的面积为2-1-(3-2 )=2
)=2 -2.
-2.
点评:本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,找到所求量的等量关系是解决问题的关键注意运用相似三角形的面积比等于相似比的平方的性质.
 -2
-2分析:阴影部分面积=S△ABG-S△COG-S△ABE.
解答:在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,故AE=
 ,
,由折叠易得△ABG为等腰直角三角形,
∴S△ABG=
 BA•AG=2,S△ABE=1,
BA•AG=2,S△ABE=1,∴CG=2BE-BC=2
 -2,
-2,∵AB∥CD,∴∠OCG=∠B=45°,
又由折叠的性质知,∠G=∠B=45°,
∴CO=OG=2-
 .∴S△COG=3-2
.∴S△COG=3-2 ,
,∴重叠部分的面积为2-1-(3-2
 )=2
)=2 -2.
-2.点评:本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,找到所求量的等量关系是解决问题的关键注意运用相似三角形的面积比等于相似比的平方的性质.

练习册系列答案
相关题目
